题目内容
如图,四边形ABCD中,∠A=∠C=900,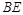 平分∠A BC交CD于E,DF平分∠A DC交AB于F
平分∠A BC交CD于E,DF平分∠A DC交AB于F
(1)若∠ABC=600,则∠ADC= °, ∠ADF= °;
(2)BE与DF平行吗?试说明理由.
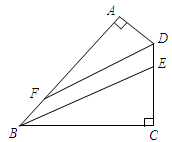
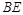 平分∠A BC交CD于E,DF平分∠A DC交AB于F
平分∠A BC交CD于E,DF平分∠A DC交AB于F(1)若∠ABC=600,则∠ADC= °, ∠ADF= °;
(2)BE与DF平行吗?试说明理由.

(1)1200,600;(2)BE∥DF.证明见解析.
试题分析:根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
(1)根据四边形内角和是3600,可以得出∠ADC=
(2)BE∥DF.
理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠CBE=∠BED=
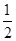 ∠ABC,∠ADF=∠FDE=
∠ABC,∠ADF=∠FDE=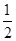 ∠ADC(角平分线的定义).
∠ADC(角平分线的定义).∴∠DFB+∠FDE=
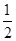 (∠ABC+∠ADC)=
(∠ABC+∠ADC)=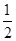 ×180°=90°(等式的性质).
×180°=90°(等式的性质).又∠CBE+∠CEB=90°(三角形的内角和等于180°),
∴∠FDE=∠CEB(等量代换).
∴BE∥DF(同位角相等,两直线平行).

练习册系列答案
相关题目

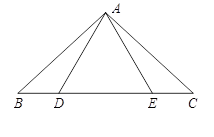
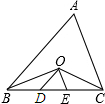

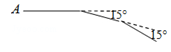

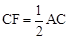 ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________