Question

先阅读，再回答问题：

如果x₁，x₂是关于x的一元二次方程ax²＋bx＋c＝0(a≠0)的两个根，那么x₁＋x₂，x₁x₂与系数a，b，c的关系是：x₁＋x₂＝－，x₁x₂＝.例如：若x₁，x₂是方程2x²－x－1＝0的两个根，则x₁＋x₂＝－＝－＝，x₁x₂＝＝＝－．

若x₁，x₂是方程2x²＋x－3＝0的两个根，（1）求x₁＋x₂，x₁x₂

(2)求＋的值．(3) 求（x₁－x₂）².

 

Answer 1

【答案】

(1) x₁+x₂=-0.5，x₁x₂=-1.5;(2)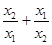=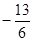;(3)（x₁－x₂）²=.

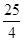【解析】

试题分析：一元二次方程ax²+bx+c=0根与系数的关系:如果方程的两个实数根是x₁,x₂，那么x₁+x₂=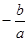，x₁x₂=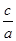,(1)由题, a=2,b=1,c=-3,x₁+x₂=-0.5，x₁x₂=-1.5;(2)通分后可以转化成两根和与乘积的式子,从而求解,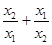==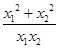=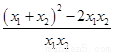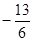;(3)去括号,利用完全平方公式a²±2ab+b²= (a±b)²)将式子转化成两根和与乘积的式子,（x₁－x₂）²=x₁²-2 x₁x₂+x₂²=（x₁+x₂）² -4 x₁x₂=.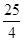

试题解析：(1)由题, a=2,b=1,c=-3,

x₁+x₂=-0.5，x₁x₂=-1.5;

(2)

=

=

=;

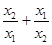
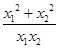
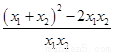
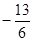(3)（x₁－x₂）²

=x₁²-2 x₁x₂+x₂²

=（x₁+x₂）² -4 x₁x₂

=.

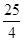考点：一元二次方程根与系数关系.