题目内容
(本题共10分) 已知关于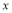 的方程
的方程 ,
,
(1)若 =1是此方程的一根,求
=1是此方程的一根,求 的值及方程的另一根;
的值及方程的另一根;
(2)试说明无论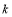 取什么实数值,此方程总有实数根.
取什么实数值,此方程总有实数根.
(1) ,另一根为-3;(2)证明见试题解析.
,另一根为-3;(2)证明见试题解析.
【解析】
试题分析:(1)先把方程的根代入方程,可以求出字母系数k值,然后根据根与系数的关系由两根之积可以求出另一个根;
(2)证明一元二次方程根的判别式恒大于0,即可解答.
试题解析:(1)把 代入方程有:
代入方程有: ,∴
,∴ .故方程为
.故方程为 ,
,
设方程的另一个根是 ,则:
,则: ,∴
,∴ .故
.故 ,方程的另一根为﹣3;
,方程的另一根为﹣3;
(2)证明:∵关于x的方程 中,△=
中,△= ,
,
∴无论 取什么实数,方程总有实数根.
取什么实数,方程总有实数根.
考点:1.一元二次方程的解;2.根的判别式;3.根与系数的关系.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目


 B、1-
B、1- C、1-
C、1- D、
D、

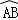 上的点D处,折痕交OA于点C,则
上的点D处,折痕交OA于点C,则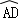 的长为 .
的长为 .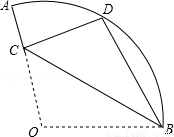
 ).
).
 .
. D.
D.