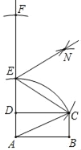
题目内容
【题目】M是正方形ABCD的边AB上一动点(不与A,B重合),BP⊥MC,垂足为P,将∠CPB绕点P旋转,得到∠C’PB’,当射线PC’经过点D时,射线PB’与BC交于点N.
(1)依题意补全图形;
(2)求证:△BPN∽△CPD;
(3)在点M的运动过程中,图中是否存在与BM始终保持相等的线段?若存在,请写出这条线段并证明;若不存在,请说明理由.
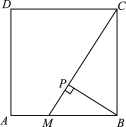
【答案】(1)见解析;(2)见解析;(3)BM=BN.
【解析】
(1)根据题意补全图形即可;
(2)由旋转性质知∠BPN=∠CPD,再由∠PCD+∠BCP=∠PBN+∠BCP=90°知∠PCD=∠PBN,从而得证;
(3)先证△MPB∽△BPC得![]() ,再由△PBN∽△PCD知
,再由△PBN∽△PCD知![]() ,从而得
,从而得![]() ,根据BC=CD可得答案.
,根据BC=CD可得答案.
(1)补全图形如图所示;
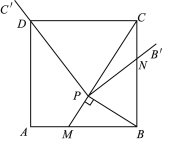
(2)证明:由旋转可得∠BPN=∠CPD.
∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠PCD+∠BCP=90°.
∵BP⊥MC,
∴∠CPB=90°.
∴∠PBC+∠PCB=90°.
∴∠PBC=∠PCD.
∴△PBN∽△PCD.
(3)答:BM=BN.
证明:∵BP⊥CM,∠MBC=90°,
∴∠MBP=∠MCB.
∴△MPB∽△BPC.
∴![]() .
.
由(2)可知△PBN∽△PCD.
∴![]() .
.
∴![]() .
.
∵BC=CD,
∴BM=BN.

 全能练考卷系列答案
全能练考卷系列答案【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示.
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -12 | -2 | 4 | 6 | 4 | … |
给出下列说法:①抛物线与y轴的交点为(0,6);②抛物线的对称轴是在y轴的右侧;③抛物线一定经过点(3,0);④当x<0时,函数值y随x的增大而减小.
从表中可知,上述说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
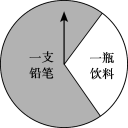
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.