题目内容
若a2-4a+4+b2-6b+9=0，试化简分式
．
| 4a3-ab2 |
| 4a2-4ab+b2 |
考点：配方法的应用,非负数的性质：偶次方,分式的值
专题：
分析：利用非负数的性质得出a、b的值，进一步整理代入求得数值即可．
解答：解：∵a2-4a+4+b2-6b+9=0，
∴（a-2）2+（b-3）2=0，
∴a-2=0，b-3=0，
∴a=2，b=3，
∴
=
=
=
=14．
∴（a-2）2+（b-3）2=0，
∴a-2=0，b-3=0，
∴a=2，b=3，
∴
| 4a3-ab2 |
| 4a2-4ab+b2 |
=
| a(2a+b)(2a-b) |
| (2a-b)2 |
=
| a(2a+b) |
| 2a-b |
=
| 2×(2×2+3) |
| 2×2-3 |
=14．
点评：此题考查配方法的运用，非负数的性质，以及分式的化简求值，注意先化简，再代入求值．
练习册系列答案
相关题目
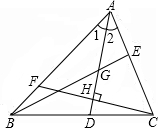如图，在△ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E．F为AB上一点，CF⊥AD于H，下面判断正确的有（ ）
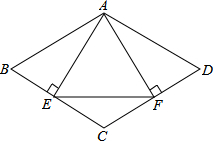如图，在菱形ABCD中，AB=4，∠C=120°，AE⊥BC于E，AF⊥CD于F，连接EF，则△AEF的面积为