题目内容
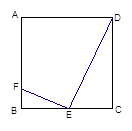
已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF=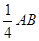 ,猜想EF与DE的位置关系,并说明理由.
,猜想EF与DE的位置关系,并说明理由.
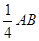 ,猜想EF与DE的位置关系,并说明理由.
,猜想EF与DE的位置关系,并说明理由.
证明见解析.
试题分析:由四边形ABCD是正方形,可得∠B=∠C=90°,AB=BC=CD,又由E是BC的中点,F在AB上,且BF=
 AB,即可证得
AB,即可证得 ,然后由两组对应边的比相等且夹角对应相等的两个三角形相似,即可证得△BEF∽△CDE,继而可求得∠DEF=90°,即可证得EF⊥DE.
,然后由两组对应边的比相等且夹角对应相等的两个三角形相似,即可证得△BEF∽△CDE,继而可求得∠DEF=90°,即可证得EF⊥DE.试题解析:EF⊥DE.理由:
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵E是BC的中点,BF=
 AB,
AB,∴BE=EC=
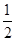 BC,
BC,∴BF=
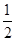 EC,BE=
EC,BE=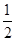 CD,
CD,∴
 ,
,∴△BEF∽△CDE,
∴∠BEF=∠CDE,
∵∠CDE+∠CED=90°,
∴∠BEF+∠CED=90°,
∴∠DEF=90°,即EF⊥DE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则OD= .
,则OD= .
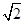 BM;
BM;