题目内容
在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．分析：根据已知得出过F作FG⊥AB于G，交CE于H，利用相似三角形的判定得出△AGF∽△EHF，再利用相似三角形的性质得出即可．
解答：
解：这种测量方法可行．
理由如下：
设旗杆高AB=x．过F作FG⊥AB于G，交CE于H（如图）．
所以△AGF∽△EHF．
因为FD=1.5，GF=27+3=30，HF=3，
所以EH=3.5-1.5=2，AG=x-1.5．
由△AGF∽△EHF，
得
=
，
即
=
，
所以x-1.5=20，
解得x=21.5（米）
答：旗杆的高为21.5米．
解：这种测量方法可行． 理由如下：
设旗杆高AB=x．过F作FG⊥AB于G，交CE于H（如图）．
所以△AGF∽△EHF．
因为FD=1.5，GF=27+3=30，HF=3，
所以EH=3.5-1.5=2，AG=x-1.5．
由△AGF∽△EHF，
得
| AG |
| EH |
| GF |
| HF |
即
| x-1.5 |
| 2 |
| 30 |
| 3 |
所以x-1.5=20，
解得x=21.5（米）
答：旗杆的高为21.5米．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△AGF∽△EHF是解题关键．
练习册系列答案
相关题目
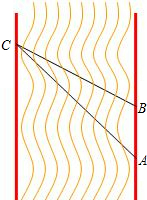在一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行20米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，帮助该同学计算出这条河的宽度．（参考数值：tan31°≈
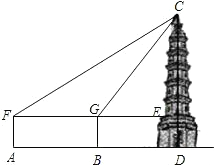时测得仰角∠CGE=37°，已知测倾器高1.5米，请你根据以上数据计算出古塔CD的高度．
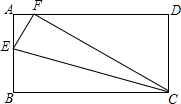在一次数学活动课上，张明同学将矩形ABCD沿直线CE折叠，顶点B恰好落在AD边上F点处，如图所示，已知CD=8cm，BE=5cm，则AD=
在一次数学活动课上，老师带领学生去测长江的宽度，某学生在长江北岸点A处观测到长江对岸水边有一点C，测得C在A东南方向上，沿长江边向东前行200米到达B处，测得C在B南偏东30°的方向上．
在一次数学活动课上，王老师给学生发了一块长40cm，宽30cm的长方形纸片（如图），要求折成一个高为5cm的无盖的且容积最大的长方体盒子．