Question

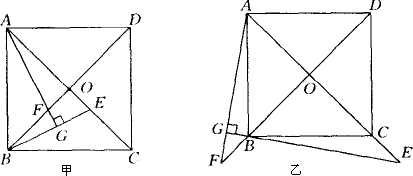
如图甲所示，已知正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，过A点作AG⊥BE，垂足为G，AG交BD于点F，则OE＝OF，若点E在AC的延长线上，AG⊥EB，交EB的延长线于点G，AG的延长线交DB的延长线于点F，其他条件不变，如图乙所示，则OE＝OF还成立吗？说明理由．

Answer 1

答案：
解析：

解：OE＝OF仍然成立．理由如下： 　　因为四边形ABCD是正方形， 　　所以∠BOE＝∠AOF＝90°，BO＝AO． 　　又因为AG⊥EB， 　　所以∠OEB＋∠EAF＝90°＝∠OFA＋∠FAE． 　　所以∠OEB＝∠OFA． 　　所以Rt△BOE≌Rt△AOF． 　　所以OE＝OF． 　　分析：若能证明△BOE≌△AOF，则结论OE＝OF成立，因此，证明△BOE≌△AOF是解题关键．