题目内容
用同样长的三根铁丝分别围成长方形、正方形、圆,其中面积最大的图形是
- A.长方形
- B.正方形
- C.圆
- D.由于不知道铁丝的长度而无法确定
C
分析:三个图形的周长相同,故可以设出其周长,从而可求出三个图形的面积,比较即可.
解答:长方形:设一边为x,S1=x( -x)=-x2+
-x)=-x2+ x,
x,
那么当x= 时,S1最大,此时S1=
时,S1最大,此时S1= ;
;
正方形:S2= ×
× =
= ;
;
圆:2πr=L,r=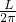 ,S3=π•r2=
,S3=π•r2=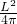 ;
;
∴S3>S2≥S1.
故选C.
点评:本题考查了圆,正方形以及长方形的周长与面积公式.
分析:三个图形的周长相同,故可以设出其周长,从而可求出三个图形的面积,比较即可.
解答:长方形:设一边为x,S1=x(
 -x)=-x2+
-x)=-x2+ x,
x,那么当x=
 时,S1最大,此时S1=
时,S1最大,此时S1= ;
;正方形:S2=
 ×
× =
= ;
;圆:2πr=L,r=
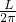 ,S3=π•r2=
,S3=π•r2=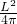 ;
;∴S3>S2≥S1.
故选C.
点评:本题考查了圆,正方形以及长方形的周长与面积公式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
用同样长的三根铁丝分别围成长方形、正方形、圆,其中面积最大的图形是( )
| A、长方形 | B、正方形 | C、圆 | D、由于不知道铁丝的长度而无法确定 |