题目内容
 在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,则BD的长为
在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,则BD的长为
- A.

- B.

- C.

- D.
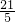
A
分析:根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到角的两边的距离相等可得点D到AB、AC上的距离相等,然后利用三角形的面积求出点D到AB的长,再利用△ABD的面积列式计算即可得解.
解答:∵∠BAC=90°,AB=3,AC=4,
∴BC= =
= =5,
=5,
∴BC边上的高=3×4÷5= ,
,
∵AD平分∠BAC,
∴点D到AB、AC上的距离相等,设为h,
则S△ABC= ×3h+
×3h+ ×4h=
×4h= ×5×
×5× ,
,
解得h= ,
,
S△ABD= ×3×
×3× =
= BD•
BD• ,
,
解得BD= .
.
故选A.
点评:本题考查了角平分线的性质,三角形的面积,勾股定理,利用三角形的面积分别求出相应的高是解题的关键.
分析:根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到角的两边的距离相等可得点D到AB、AC上的距离相等,然后利用三角形的面积求出点D到AB的长,再利用△ABD的面积列式计算即可得解.
解答:∵∠BAC=90°,AB=3,AC=4,
∴BC=
 =
= =5,
=5,∴BC边上的高=3×4÷5=
 ,
,∵AD平分∠BAC,
∴点D到AB、AC上的距离相等,设为h,
则S△ABC=
 ×3h+
×3h+ ×4h=
×4h= ×5×
×5× ,
,解得h=
 ,
,S△ABD=
 ×3×
×3× =
= BD•
BD• ,
,解得BD=
 .
.故选A.
点评:本题考查了角平分线的性质,三角形的面积,勾股定理,利用三角形的面积分别求出相应的高是解题的关键.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.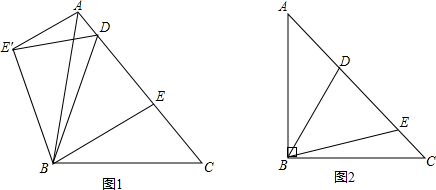
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.