题目内容
|m|=m+1,则(4m+1)2004=分析:本题可根据条件|m|=m+1进行分析,m的取值可分三种条件讨论,m为正数,m为负数,m为0,讨论可得m的值,代入计算即可.
解答:解:根据题意,可得m的取值有三种,分别是:
m为正数,则|m|=m+1可转换为m=m+1,此种情况不成立.
m为0,则|m|=m+1可转换为0=0+1,此种情况不成立.
m为负数,则|m|=m+1可转换为-m=m+1,可得m值为-
.
将m的值代入,则可得(4m+1)2004=(4×-
+1)2004=1.
故答案为:1.
m为正数,则|m|=m+1可转换为m=m+1,此种情况不成立.
m为0,则|m|=m+1可转换为0=0+1,此种情况不成立.
m为负数,则|m|=m+1可转换为-m=m+1,可得m值为-
| 1 |
| 2 |
将m的值代入,则可得(4m+1)2004=(4×-
| 1 |
| 2 |
故答案为:1.
点评:本题考查代数式的求值,根据题意求出m的值,代入计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
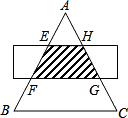 如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的( )
如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
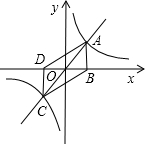 如图,正比例函数y=x与反比例
如图,正比例函数y=x与反比例 10、如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
10、如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )