题目内容
已知一平面内的任意四点,其中任何三点都不在一条直线上,试问:是否一定能从这样的四点中选出三点构成一个三角形,使得这个三角形至少有一内角不大于45°?请证明你的结论.
 证明:能.
证明:能.(1)如图a,若四点A,B,C,D构成凸四边形.则必有一个内角≤90°.不妨设为∠A.
这是因为,假设四个内角都大于90°,则360°=∠A+∠B+∠C+∠D>4×90°=360°.矛盾.
则∠BAC+∠CAD≤90°.
则∠BAC与∠CAD中必有一个≤
 ×90°=45°.
×90°=45°.故结论成立.
(2)如图b.若四点A,B,C,D构成四边形.则△ABC中必有一个内角≤
 ×180°=60°.
×180°=60°.不防设∠A≤60°.
又∠A=∠BAD+∠CAD≤60°.
则∠BAD与∠CAD值中必有一个≤
 ×60°<45°.
×60°<45°.故结论成立.
分析:结论是以疑问形式出现的,不妨先假定是肯定的,然后推理.若推出矛盾,则说明结论是否定的;若推不出矛盾,则可考虑去证明结论是肯定的.
点评:本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 先阅读短文,再回答短文后面的问题.
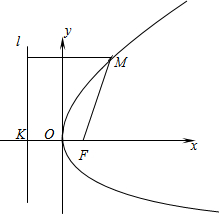
先阅读短文,再回答短文后面的问题.平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线.
下面根据抛物线的定义,我们来求抛物线的方程.
如上图,建立直角坐标系xoy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合.设|KF|=p(p>0),那么焦点F的坐标为(
| p |
| 2 |
| p |
| 2 |
设点M(x,y)是抛物线上任意一点,点M到l的距离为d,由抛物线的定义,抛物线就是满足|MF|=d的点M的轨迹.
∵|MF|=
(x-
|
| p |
| 2 |
(x-
|
| p |
| 2 |
将上式两边平方并化简,得y2=2px(p>0)①
方程①叫做抛物线的标准方程,它表示的抛物线的焦点在x轴的正半轴上,坐标是(
| p |
| 2 |
| p |
| 2 |
一条抛物线,由于它在坐标平面内的位置不同,方程也不同.所以抛物线的标准方程还有其它的几种形式:y2=-2px,x2=2py,x2=-2py.这四种抛物线的标准方程,焦点坐标以及准线方程列表如下:
| 标准方程 | 交点坐标 | 准线方程 | ||||
| y2=2px(p>0) | (
|
x=-
| ||||
| y2=-2px(p>0) | (-
|
x=
| ||||
| x2=2py(p>0) | (0,
|
y=-
| ||||
| x2=-2py(p>0) | (0,-
|
y=-
|
(1)①已知抛物线的标准方程是y2=8x,则它的焦点坐标是
②已知抛物线的焦点坐标是F(0,-6),则它的标准方程是
(2)点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
(3)直线y=
| 3 |
 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题.
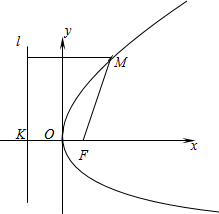
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线.
下面根据抛物线的定义,我们来求抛物线的方程.
如上图,建立直角坐标系xoy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合.设|KF|=p(p>0),那么焦点F的坐标为( ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.
设点M(x,y)是抛物线上任意一点,点M到l的距离为d,由抛物线的定义,抛物线就是满足|MF|=d的点M的轨迹.
∵|MF|=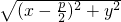 ,d=|x+
,d=|x+ |∴
|∴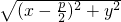 =|x+
=|x+ |
|
将上式两边平方并化简,得y2=2px(p>0)①
方程①叫做抛物线的标准方程,它表示的抛物线的焦点在x轴的正半轴上,坐标是( ,0),它的准线方程是x=-
,0),它的准线方程是x=- .
.
一条抛物线,由于它在坐标平面内的位置不同,方程也不同.所以抛物线的标准方程还有其它的几种形式:y2=-2px,x2=2py,x2=-2py.这四种抛物线的标准方程,焦点坐标以及准线方程列表如下:
| 标准方程 | 交点坐标 | 准线方程 |
| y2=2px(p>0) | (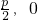 ) ) | x=- |
| y2=-2px(p>0) | (-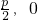 ) ) | x= |
| x2=2py(p>0) | (0, ) ) | y=- |
| x2=-2py(p>0) | (0,- ) ) | y=- |
(1)①已知抛物线的标准方程是y2=8x,则它的焦点坐标是______,准线方程是______
②已知抛物线的焦点坐标是F(0,-6),则它的标准方程是______.
(2)点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
(3)直线
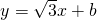 经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.
经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长. 