题目内容
已知x-1=
,先化简代数式(
-
)÷
,再求这个代数式的值.
| 2 |
| x-1 |
| x2-x |
| x |
| x2-2x+1 |
| 1 |
| x |
分析:首先把括号内的分式进行通分,进行加法运算,然后把除法转化成乘法,进行乘法运算,然后把已知的式子变形为x=
+1,代入化简以后的式子即可求解.
| 2 |
解答:解:原式=【
-
】•x
=1-
=
-
=
,
∵x-1=
,
则x=
+1,则原式=
=
.
| x-1 |
| x(x-1) |
| x |
| (x-1)2 |
=1-
| x2 |
| (x-1)2 |
=
| (x-1)2 |
| (x-1)2 |
| x2 |
| (x-1)2 |
=
| 1-2x |
| (x-1)2 |
∵x-1=
| 2 |
则x=
| 2 |
1-2(
| ||
| 2 |
-2
| ||
| 2 |
点评:本题考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 +|4-b|=0,先化简,再求值.
+|4-b|=0,先化简,再求值.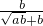 +
+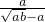 )÷
)÷ .
.