题目内容
4. 如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.
如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.(1)求线段AD的长度;
(2)∠BCD是直角吗?请说明你的理由.
分析 (1)直接利用勾股定理求出AD的长度;
(2)利用勾股定理求出线段DC、BC和BD的长,再利用勾股定理逆定理证明△BCD是直角三角形即可.
解答  解:(1)AD=$\sqrt{{3}^{2}+{4}^{2}}$=5;
解:(1)AD=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(2)∠BCD是直角.
理由:连接BD,
∵DC2=12+22=5,
BC2=22+42=20,
BD2=32+42=25,
∴CD2+BC2=BD2,
∴△BCD是直角三角形,
∴∠BCD是直角.
点评 本题主要考查了勾股定理以及逆定理的知识,解答此题的关键是熟练掌握勾股定理以及逆定理,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列命题中,真命题的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直平分的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
19. 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
9.若点A(2,n)在x轴上,则点B(-2,n+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列事件中,发生概率最小的事件的是( )
| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.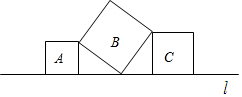 如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.
如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.