Question

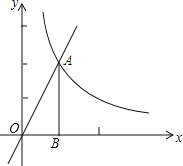
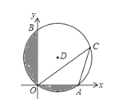
【题目】如图，在平面直角坐标系中，已知⊙D经过原点O，与x轴、y轴分别交于A、B两点，B点坐标为（0，），OC与⊙D交于点C，∠OCA＝30°.求

（1）⊙D的半径；

（2）圆中阴影部分的面积（结果保留根号和π）

Answer 1

【答案】（1）；（2）

【解析】

（1）连接AB，根据∠AOB=90°，得到AB为⊙D直径，∠ABO=∠C=30°，根据直角三角形中，30°角所对的直角边是斜边的一半可得，AB=2AO=2DA，利用勾股定理求得AB的值，进而求得⊙D的半径；

（2）S阴影=S半圆+S△AOB，即可解答.

（1）连接AB，

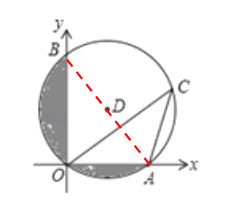
∵∠AOB=90°，∴AB为⊙D直径

∠ABO与∠C是同弧所对圆周角，

∴ ∠ABO=∠C=30°

∴AB=2AO=2DA，∵B点坐标为（0，）， ∴OB=

在直角三角形AOB中，AB2=OA2+OB2,∴AB2=(AB)2+（）2

∵AB＞0，∴AB=，即⊙D的半径为

（2）解：由（1）可知，AB为⊙D直径，OA=

S阴影=S半圆+S△AOB