题目内容
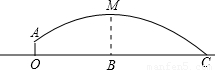
如图,一场足球比赛中,守门员站立在O点,将对方射来的足球凌空反射回去,球从离地面l米的A处飞出,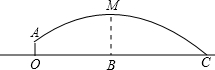 运行轨迹是一条抛物线.运动员甲在距O点6米的B处发现球在自己的正上方达到最高点M,距离地面4米.
运行轨迹是一条抛物线.运动员甲在距O点6米的B处发现球在自己的正上方达到最高点M,距离地面4米.
(1)请你建立适当的直角坐标系,并求出此抛物线的表达式;
(2)足球落地点C距守门员多远?(取 ≈1.7)
≈1.7)
 解:(1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系.
解:(1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系.由于抛物线的顶点是(6,4),
所以设抛物线的表达式为y=a(x-6)2+4,
当x=0,y=1时,1=a(0-6)2+4,
所以
 ,
,所以抛物线解析式为:y=-
 x2+x+1;
x2+x+1;(2)令y=0,则-
 x2+x+1=0,
x2+x+1=0,解得:
 (舍去),
(舍去), =12.8(米),
=12.8(米),所以,足球落地点C距守门员约12.8米.
分析:(1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系,得出抛物线的顶点是(6,4),利用顶点式求出解析式即可;
(2)利用令y=0,则-
 x2+x+1=0,求出图象与x轴交点坐标即可得出答案.
x2+x+1=0,求出图象与x轴交点坐标即可得出答案.点评:此题主要考查了顶点式求二次函数解析式以及一元二次方程的解法等知识,正确建立坐标系得出解析式是解题关键.

练习册系列答案
相关题目
 13、如图,在一场足球比赛中,球员A欲传球给同伴B,对方球员C意图抢断传球,已知球速为16m/s,球员速度为8m/s.当球由A传出的同时,球员C选择与AC垂直的方向出击,恰好在点D处将球成功抢断,则角θ=
13、如图,在一场足球比赛中,球员A欲传球给同伴B,对方球员C意图抢断传球,已知球速为16m/s,球员速度为8m/s.当球由A传出的同时,球员C选择与AC垂直的方向出击,恰好在点D处将球成功抢断,则角θ=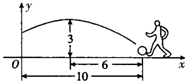 (2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
(2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米. 运行轨迹是一条抛物线.运动员甲在距O点6米的B处发现球在自己的正上方达到最高点M,距离地面4米.
运行轨迹是一条抛物线.运动员甲在距O点6米的B处发现球在自己的正上方达到最高点M,距离地面4米. ≈1.7)
≈1.7)