题目内容
△ABC中，M为BC上一点，AM是∠BAC的平分线，若AB=2，AC=1，BM=| 3 | 2 |
分析：过C作CD∥MA，交BA的延长线于D，根据题意先证出AM∥CD，再利用比例的性质可得出答案．
解答：
解：如图，过C作CD∥MA，交BA的延长线于D，则∠BAM=∠ADC，∠MAC=∠ACD，
∵∠BAM=∠MAC，
∴∠ADC=∠ACD，
∴AC=AD，AD=1，
∴AM∥CD，
∴
=
，
∴CM=
=
．
故答案为：
．
解：如图，过C作CD∥MA，交BA的延长线于D，则∠BAM=∠ADC，∠MAC=∠ACD，∵∠BAM=∠MAC，
∴∠ADC=∠ACD，
∴AC=AD，AD=1，
∴AM∥CD，
∴
| CM |
| BM |
| AD |
| AB |
∴CM=
| BM•AD |
| AB |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查了平行线分线段成比例的知识，有一定难度，关键是根据题意证明出AM∥CD．
练习册系列答案
相关题目
如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=4，CE=| 4 |
| 3 |
A、8
| ||
| B、15 | ||
C、9
| ||
D、12
|
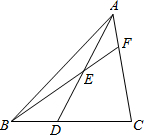（2012•泰顺县模拟）如图，在△ABC中，D为BC上的一点，E为AD上的一点，BE的延长线交AC于点F，已知
已知：如图，在△ABC中，D为BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F，且BE=CF．
如图，在△ABC中，D为BC边上的一点，已知AB=13，AD=12，AC=15，BD=5，求CD的长．