Question

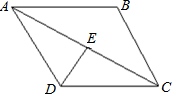如图，CD∥AB，∠ADC=120°，AC平分∠DAB，DE⊥AC，则∠DCA=________．如果DE=5cm，则AD=________cm．

Answer 1

30°    10
分析：根据平行线和角平分线的性质可得∠DAC=∠DCA，根据三角形内角和公式即可求出∠DCA的度数；在Rt△ADE中，运用含30度角的直角三角形的性质可得AD的长度．
解答：∵CD∥AB，
∴∠BAC=∠ACD，
∵AC平分∠DAB，
∴∠BAC=∠DAC，
∴∠DAC=∠ACD，
∵∠ADC=120°，
∴∠DCA=（180°-120°）÷2=30°．
∵DE⊥AC，DE=5cm，
∴在Rt△ADE中，AD=2DE=10cm．
故答案为：30°，10．
点评：本题综合考查了平行线和角平分线的性质，含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．得到∠DAC=∠ACD是解题的关键．