题目内容
 (2013•海珠区一模)随着经济发展,污染问题日益严重.某环保厂家看到这个商机,以200万元购买了某项空气净化产品的生产技术后,再投入280万元购买生产设备进行该产品的生产.已知生产这种产品的成本价为每件30元,经过市场调研发现,该产品的销售单价定在40到50元之间较为合理,并且该产品的年销售量y(万件)与销售单价x(元)之间的关系如图所示.
(2013•海珠区一模)随着经济发展,污染问题日益严重.某环保厂家看到这个商机,以200万元购买了某项空气净化产品的生产技术后,再投入280万元购买生产设备进行该产品的生产.已知生产这种产品的成本价为每件30元,经过市场调研发现,该产品的销售单价定在40到50元之间较为合理,并且该产品的年销售量y(万件)与销售单价x(元)之间的关系如图所示.(1)请根据图象直接写出销售单价是45元时的年销售量;
(2)求出年销售量y(万件)与销售单价x(元)之间的函数关系式;
(3)求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式;并说明投资的第一年,销售单价定为多少时该厂家能获得最大盈利?最大利润是多少?
分析:(1)根据图象,找出单价45元时对应的y值;
(2)分别在图象上找出当40<x<45和45<x<50时点的坐标,设出函数关系式,代入点的坐标,求出函数关系式;
(3)根据年获利=销售量×(单价-成本价)-200-280列出函数关系式,求出最大盈利即可.
(2)分别在图象上找出当40<x<45和45<x<50时点的坐标,设出函数关系式,代入点的坐标,求出函数关系式;
(3)根据年获利=销售量×(单价-成本价)-200-280列出函数关系式,求出最大盈利即可.
解答:解:(1)根据图象可得:销售单价是45元时的年销售量是30万件.
(2)当40≤x≤45时,设函数关系式为y=kx+b,
分别代入(40,40)和(45,30),
得:
,
解得:
,
故函数关系式为:y=-2x+120;
当45<x≤50时,设函数关系式为y=mx+n,
分别代入(45,30)和(50,25),
得:
,
解得:
,
故函数关系式为:y=-x+75;
所以年销售量y(万件)与销售单价x(元)之间的函数关系式为:y=
;
(3)该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式为:
W=(x-30)y-200-280=
,
当40≤x≤45时,
W=-2x2+180x-4080=-2(x-45)2-30,
开口向下,有最大值,
当x=45时,Wmax=-30,
故此时厂家不管如何定销售单价,都不可能盈利,
当45<x≤50时,
W=-x2+105x-2730=-(x-52.5)2+26,
开口向下,对称轴为x=52.5,
故当x=50时,W有最大值Wmax=20,
答:销售单价定为50元时,厂家能获得最大盈利,最大利润是20万元.
(2)当40≤x≤45时,设函数关系式为y=kx+b,
分别代入(40,40)和(45,30),
得:
|
解得:
|
故函数关系式为:y=-2x+120;
当45<x≤50时,设函数关系式为y=mx+n,
分别代入(45,30)和(50,25),
得:
|
解得:
|
故函数关系式为:y=-x+75;
所以年销售量y(万件)与销售单价x(元)之间的函数关系式为:y=
|
(3)该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式为:
W=(x-30)y-200-280=
|
当40≤x≤45时,
W=-2x2+180x-4080=-2(x-45)2-30,
开口向下,有最大值,
当x=45时,Wmax=-30,
故此时厂家不管如何定销售单价,都不可能盈利,
当45<x≤50时,
W=-x2+105x-2730=-(x-52.5)2+26,
开口向下,对称轴为x=52.5,
故当x=50时,W有最大值Wmax=20,
答:销售单价定为50元时,厂家能获得最大盈利,最大利润是20万元.
点评:本题考查了二次函数的应用,涉及到分段函数,难度较大,解答本题的关键是结合图形求出x的不同范围时的不同解析式,并熟练掌握运用配方法求二次函数的最大值.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
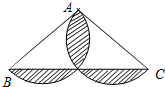 (2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
(2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )