Question

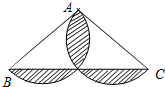（2013•海珠区一模）如图，在△ABC中，AB=AC=5，CB=8，分别以AB、AC为直径作半圆，则图中阴影部分面积是（　　）

• A．

  25

  4

  π-24
• B．25π-24
• C．25π-12
• D．

  25

  4

  π-12

Answer 1

分析：设以AB、AC为直径作半圆交BC于D点，连AD，根据直径所对的圆周角为直角得到AD⊥BC，再根据勾股定理计算出AD，然后利用阴影部分面积=半圆AC的面积+半圆AB的面积-△ABC的面积计算即可．

解答：解：设以AB、AC为直径作半圆交BC于D点，连AD，如图，
∴AD⊥BC，
∴BD=DC=

1

2

BC=4，
∵AB=AC=5，
∴AD=3，
∴阴影部分面积=半圆AC的面积+半圆AB的面积-△ABC的面积
=π×（

5

2

）²-

1

2

×8×3
=

25

4

π-12．
故选：D．

点评：本题考查了不规则图形面积的计算方法：把不规则的图形面积的计算转化为规则图形的面积和差来计算．也考查了圆周角定理的推论以及勾股定理．