Question

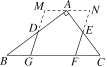
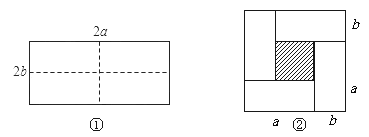
【题目】如图1，分别沿矩形纸片ABCD和正方形EFGH纸片的对角线AC，EG剪开，拼成如图2所示的平行四边形KLMN，若中间空白部分恰好是正方形OPQR．

（1）若AB=m，BC=n，用含m、n的代数式表示正方形EFGH的边长；

（2）若正方形EFGH的面积为25，求平行四边形KLMN的面积；

（3）平行四边形KLMN是否能为菱形？请说明理由．

Answer 1

【答案】（1）；（2）50；（3）不能，理由见解析．

【解析】

（1）设正方形的边长为，则：，，根据四边形EFGH是正方形，得到，即有，，利用可以得到结果；

（2）设正方形的边长为，根据正方形面积为25，可得，，据此可得平行四边形KLMN的面积．

（3）利用反证法，假设是菱形，则，正方形的边长为，可求出m=n，则小正方形ROPQ边长为0，与题目描述相矛盾，所以假设不成立，不是菱形．

（1）设正方形的边长为，

则：，，、

∵四边形EFGH是正方形，

∴，即有

∴，

∴

（2）设正方形的边长为，

∵正方形面积为25，

∴正方形边长为5，

∴，，

∴平行四边形KLMN的面积．

（3）结论：不能．

证明：假设是菱形，则，正方形的边长为，

于是有，

则，即，则m=n，

则小正方形ROPQ边长为0，与题目描述相矛盾．所以假设不成立，不是菱形．