题目内容
已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点做CD⊥直线AP于D,且CD是⊙O的切线,试求PD:AB的值为多少?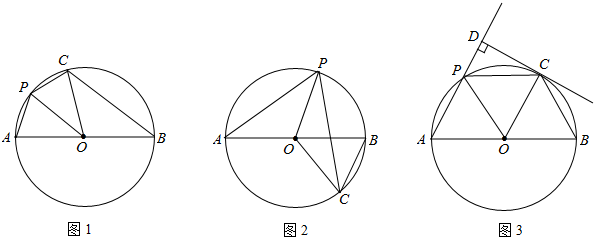
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点做CD⊥直线AP于D,且CD是⊙O的切线,试求PD:AB的值为多少?

考点:圆的综合题
专题:
分析:(1)利用对折的性质得到△OAP≌△OCP,则∠1=∠2,根据三角形外角性质得∠1+∠2=∠B+∠OCB,于是可得到∠2=∠B,然后根据平行线的判定定理得到PO∥BC;
(2)由△OAP≌△OCP得到∠1=∠2,而∠A=∠2,则∠A=∠3,根据圆周角定理得到∠A=∠3,则∠1=∠3,然后根据平行线的判定定理得到PO∥BC;
(3)根据切线的性质得OC⊥CD,易得OC∥AD,则∠2=∠4,∠A=∠3,而∠A=∠4,所以∠2=∠3,利用OP∥BC同理得到∠3=∠5,则可判断△OBC为等边三角形,所以∠3=∠2=60°,于是可判断△OPC也为等边三角形,得到∠6=60°,PC=OC,可计算出∠7=30°,根据含30度的直角三角形三边的关系得PD=
PC,
由此易得PD:AB=1:4.
(2)由△OAP≌△OCP得到∠1=∠2,而∠A=∠2,则∠A=∠3,根据圆周角定理得到∠A=∠3,则∠1=∠3,然后根据平行线的判定定理得到PO∥BC;
(3)根据切线的性质得OC⊥CD,易得OC∥AD,则∠2=∠4,∠A=∠3,而∠A=∠4,所以∠2=∠3,利用OP∥BC同理得到∠3=∠5,则可判断△OBC为等边三角形,所以∠3=∠2=60°,于是可判断△OPC也为等边三角形,得到∠6=60°,PC=OC,可计算出∠7=30°,根据含30度的直角三角形三边的关系得PD=
| 1 |
| 2 |
由此易得PD:AB=1:4.
解答:解:(1)如图1,
∵△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
∴△OAP≌△OCP,
∴∠1=∠2,
∵∠1+∠2=∠B+∠OCB,
而OC=OB,
∴∠B=∠OCB,
∴∠2=∠B,
∴PO∥BC;
(2)结论仍然成立.理由如下:
∵△OAP≌△OCP,
∴∠1=∠2,
∵OP=OA,
∴∠A=∠2,
∵∠A=∠3,
∴∠1=∠3,
∴PO∥BC;
(3)∵CD为是⊙O的切线,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠2=∠4,∠A=∠3,
而∠A=∠4,
∴∠2=∠3,
∵OP∥BC,
∴∠2=∠5,
∴∠3=∠5,
∴△OBC为等边三角形,
∴∠3=∠2=60°,
∴△OPC为等边三角形,
∴∠6=60°,PC=OC,
∴∠7=30°,
∴PD=
PC,
∴PD=
OC=
AB,即PD:AB=1:4.

∵△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
∴△OAP≌△OCP,
∴∠1=∠2,
∵∠1+∠2=∠B+∠OCB,
而OC=OB,
∴∠B=∠OCB,
∴∠2=∠B,
∴PO∥BC;
(2)结论仍然成立.理由如下:
∵△OAP≌△OCP,
∴∠1=∠2,
∵OP=OA,
∴∠A=∠2,
∵∠A=∠3,
∴∠1=∠3,
∴PO∥BC;
(3)∵CD为是⊙O的切线,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠2=∠4,∠A=∠3,
而∠A=∠4,
∴∠2=∠3,
∵OP∥BC,
∴∠2=∠5,
∴∠3=∠5,
∴△OBC为等边三角形,
∴∠3=∠2=60°,
∴△OPC为等边三角形,
∴∠6=60°,PC=OC,
∴∠7=30°,
∴PD=
| 1 |
| 2 |
∴PD=
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理、切线的性质以及平行线的判定与性质;运用等边三角形的性质和含30度的直角三角形三边的关系进行几何计算.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
下列各组图形中,哪一组图形中AD是△ABC的高( )
A、 |
B、 |
C、 |
D、 |
已知正整数a、b、c,a≤b<c,c最大为6,存在以a、b、c为三边长的三角形的个数为( )
| A、10 | B、12 | C、13 | D、14 |
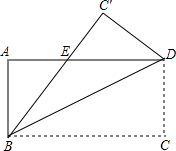 如图平行四边形ABCD中,∠C=90度,沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=16,AB=8,则DE的长
如图平行四边形ABCD中,∠C=90度,沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=16,AB=8,则DE的长 如图所示,动点C在⊙O的弦AB上运动,AB=
如图所示,动点C在⊙O的弦AB上运动,AB= 小明想测量在太阳光下一栋楼高,他设计了一种测量方案如下:如图,小明站到点E处时,刚好使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,小明测得落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
小明想测量在太阳光下一栋楼高,他设计了一种测量方案如下:如图,小明站到点E处时,刚好使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,小明测得落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m). 如图,在小长方形组成的网格中,每个小长方形的长为2,宽为1,A、B两点在网格的格点上,若点C也在网格的格点上,且△ABC是等腰三角形,则满足条件的点C的个数是( )
如图,在小长方形组成的网格中,每个小长方形的长为2,宽为1,A、B两点在网格的格点上,若点C也在网格的格点上,且△ABC是等腰三角形,则满足条件的点C的个数是( )