题目内容
如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC= 度.


90
【考点】平行线的性质.
【专题】综合题.
【分析】延长AE交CD于点F,根据两直线平行同旁内角互补可得∠BAE+∠EFC=180°,已知∠BAE的度数,不难求得∠EFC的度数,再根据三角形的外角的性质即可求得∠AEC的度数.
【解答】解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°.
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故答案为90.


【点评】此题主要考查学生对平行线的性质及三角形的外角性质的综合运用,注意辅助线的添加方法.

练习册系列答案
相关题目
 B.
B.
 D.
D.

 )﹣1.
)﹣1. 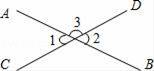




 ﹣
﹣

 ,4,
,4,
 ,2π,0.15,
,2π,0.15,
 中,有理数的个数为B,无理数的个数为A,则A﹣B的值为( )
中,有理数的个数为B,无理数的个数为A,则A﹣B的值为( ) 个图案中有白色地面砖的块数为______。
个图案中有白色地面砖的块数为______。

