计算-13 (2)-64÷3$\frac{1}{5}$×1$\frac{1}{4}$3-|-$\frac{1}{16}$|×(-4)(4)($\frac{1}{4}$-$\frac{1}{6}$-$\frac{1}{12}$)×24．题目和参考答案——青夏教育精英家教网—

题目内容

10．计算
（1）-20+（-14）-（-18）-13
（2）-64÷3$\frac{1}{5}$×1$\frac{1}{4}$
（3）-16÷（-2）³-|-$\frac{1}{16}$|×（-4）
（4）（$\frac{1}{4}$-$\frac{1}{6}$-$\frac{1}{12}$）×24．

分析（1）原式利用减法法则变形，计算即可得到结果；
（2）原式从左到右依次计算即可得到结果；
（3）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；
（4）原式利用乘法分配律计算即可得到结果．

解答解：（1）原式=-20-14+18-13=-29；
（2）原式=-64×$\frac{5}{16}$×$\frac{5}{4}$=-25；
（3）原式=-16÷（-8）-$\frac{1}{16}$×（-4）=2$\frac{1}{4}$；
（4）原式=6-4-2=0．

点评此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

相关题目

20．计算-2÷（-2²）=$\frac{1}{2}$．

1．如图1，在直角梯形ABCD中，∠A=∠B=90°，AD∥BC，AB=AD=3，BC=9，点P、Q同时从点B出发，沿射线BC向右匀速运动，已知点Q移动速度是点P速度的3倍，以PQ为一边在BC上方作正方形PQMN，设点P移动距离为x（x＞0），当点P与点C重合时，P、Q同时停止运动．

（1）正方形PQMN的边长是2x（用含x的代数式表示），tan∠BCD=$\frac{1}{2}$．
（2）当点M移动至线段CD上，试求此时x的值．
（3）若正方形PQMN与梯形ABCD的重叠部分面积为y，求y与x之间的函数关系式．

18．

已知线段a、b，用圆规和直尺画线段AC，使它等于AC=2a+b．（保留作图痕迹，并写出简要作法）

5．平方得1的数是±1，立方得-64的数是-4．

15．（1）抛物线y=kx²+（2k+1）x+2图象与x轴的两个交点为$-\frac{1}{k}$，-2
（2）若（1）中两个交点的横坐标均为整数，且k为正整数，试求出该二次函数的表达式；
（3）已知抛物线y=kx²+（2k+1）x+2恒过定点，直接写出定点的坐标．

2．已知：ab≠0，且M=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|ab|}{ab}$，当a、b取不同的值时，M有（　　）

19．

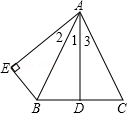已知：如图，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E．
（1）求证：AD=AE；
（2）求证：∠DAE=∠BAC；
（2）若∠2=30°，试判断△ABC的形状，并说明理由．

20．

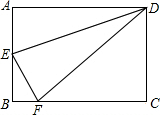如图，长方形ABCD中，点E在边AB上，将长方形ABCD沿直线DE折叠，点A恰好落在边BC上的点F处，若AE=5cm，BF=3cm，则CD的长度是（　　）

试题分类