题目内容
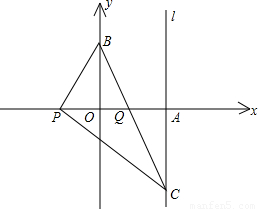
(2002•绍兴)如图,已知平面直角坐标系中三点A(4,0),(0,4),P(x,0)(x<0),作PC⊥PB交过点A的直线l于点C(4,y).(1)求y关于x的函数解析式;
(2)当x取最大整数时,求BC与PA的交点Q坐标.
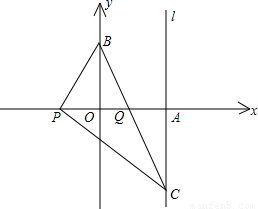
【答案】分析:(1)根据题已知点的坐标和图中几何关系,要求y关于x的函数解析式,得找到相似三角形,由图中垂直条件易知△BOP∽△PAC,再根据比例关系求出y关于x的函数解析式;
(2)由(1)知函数y的解析式,把x取最大整数时的值代入求得y的值,从而求出Q点坐标.
解答:解:(1)∵BO⊥PO,PC⊥PB,
∴∠PBO+∠BPO=90°,∠BPO+∠APC=90°,
∴∠PBO=∠APC,
∵A(4,0),C(4,y)在l上,
∴∠BOP=∠PAC=90°,
∴△BOP∽△PAC(两角对应相等,两三角形相似),
∴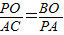 ,
,
∴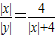 ,
,
∵x<0,y<0,
∴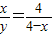 ,
,
∴y=- x2+x;
x2+x;
(2)∵x<0,且x取最大整数,
∴x=-1,
此时y=- ×(-1)2-1=-
×(-1)2-1=- ,
,
∵BO∥l,
∴△BOQ∽△CAQ,
∴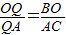 ,
,
设Q(a,0),有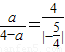 ,5a=16(4-a),
,5a=16(4-a),
∴a=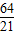 ,
,
∴Q点的坐标为(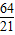 ,0).
,0).
点评:此题考查一次函数的性质及相似三角形的性质,第一问较新颖,求出函数的关系式,为下题作铺垫,同时又转化为求函数最值的问题.
(2)由(1)知函数y的解析式,把x取最大整数时的值代入求得y的值,从而求出Q点坐标.
解答:解:(1)∵BO⊥PO,PC⊥PB,
∴∠PBO+∠BPO=90°,∠BPO+∠APC=90°,
∴∠PBO=∠APC,
∵A(4,0),C(4,y)在l上,
∴∠BOP=∠PAC=90°,
∴△BOP∽△PAC(两角对应相等,两三角形相似),
∴
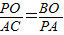 ,
,∴
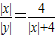 ,
,∵x<0,y<0,
∴
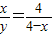 ,
,∴y=-
 x2+x;
x2+x;(2)∵x<0,且x取最大整数,
∴x=-1,
此时y=-
 ×(-1)2-1=-
×(-1)2-1=- ,
,∵BO∥l,
∴△BOQ∽△CAQ,
∴
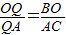 ,
,设Q(a,0),有
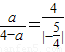 ,5a=16(4-a),
,5a=16(4-a),∴a=
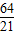 ,
,∴Q点的坐标为(
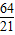 ,0).
,0).点评:此题考查一次函数的性质及相似三角形的性质,第一问较新颖,求出函数的关系式,为下题作铺垫,同时又转化为求函数最值的问题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
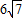 π
π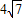 π
π