题目内容
 如图所示的一块地,AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
如图所示的一块地,AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
分析:连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差.
解答: 解:连接AC,则在Rt△ADC中,
解:连接AC,则在Rt△ADC中,
AC2=CD2+AD2=122+92=225,
∴AC=15,在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC-S△ACD=
AC•BC-
AD•CD=
×15×36-
×12×9=270-54=216.
答:这块地的面积是216平方米.
 解:连接AC,则在Rt△ADC中,
解:连接AC,则在Rt△ADC中,AC2=CD2+AD2=122+92=225,
∴AC=15,在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:这块地的面积是216平方米.
点评:解答此题的关键是通过作辅助线使图形转化成特殊的三角形,可使复杂的求解过程变得简单.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
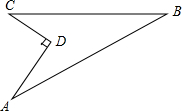 如图所示的一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,这块地的面积为
如图所示的一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,这块地的面积为 如图所示的一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,则这块地的面积为
如图所示的一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,则这块地的面积为 如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,BC=12m,AB=13m.求这块地的面积.
如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,BC=12m,AB=13m.求这块地的面积. 如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.
如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.