题目内容
4.若第二象限的点P(a,b)到x轴的距离是4+a,到y轴的距离是b-1,则点P的坐标为(-$\frac{3}{2}$,$\frac{5}{2}$).分析 根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度列出方程组,然后求解即可.
解答 解:∵点P(a,b)在第二象限,
∴a<0,b>0,
∵点到x轴的距离是4+a,到y轴的距离是b-1,
∴$\left\{\begin{array}{l}{4+a=b}\\{b-1=-a}\end{array}\right.$,
解方程组得,$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
所以,点P的坐标为(-$\frac{3}{2}$,$\frac{5}{2}$).
故答案为:(-$\frac{3}{2}$,$\frac{5}{2}$).
点评 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
15.二次根式$\sqrt{x-1}$中字母x的取值范围是( )
| A. | x<1 | B. | x≥1 | C. | x≤0 | D. | x≥0 |
19.以下问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对招聘人员的面试 | ||
| C. | 了解一批灯泡的使用寿命 | D. | 了解701班的身高情况 |
9.某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20%,并补全直方图;
(2)扇形统计图中“C组”所对应的圆心角的度数是90度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.
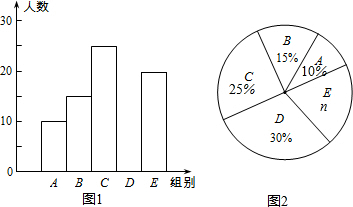
根据以上信息解决下列问题:
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | 20 |
(2)扇形统计图中“C组”所对应的圆心角的度数是90度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.

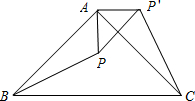 △ABC为直角三角形,∠BAC=90°,将△ABP旋转后与△ACP重合,AP=a,求PP′.
△ABC为直角三角形,∠BAC=90°,将△ABP旋转后与△ACP重合,AP=a,求PP′.