题目内容
 如图所示,直角三角形三边上的半圆面积从小到大依次记为S1、S2、S3,则S1、S2、S3的关系是( )
如图所示,直角三角形三边上的半圆面积从小到大依次记为S1、S2、S3,则S1、S2、S3的关系是( )分析:设三个半圆的直径分别为:d1、d2、d3,半圆的面积=
π×(
)2,将d1、d2、d3代入分别求出S1、S2、S3,由勾股定理可得:d12+d22=d32,观察三者的关系即可.
| 1 |
| 2 |
| 直径 |
| 2 |
解答:解:设三个半圆的直径分别为:d1、d2、d3,
S1=
×π×(
)2=
π,
S2=
×π×(
)2=
π,
S3=
×π×(
)2=
π.
由勾股定理可得:
d12+d22=d32,
∴S1+S2=
(d12+d22)=
π=S3,
所以S1、S2、S3的关系是:S1+S2=S3.
故选A.
S1=
| 1 |
| 2 |
| d1 |
| 2 |
| d12 |
| 8 |
S2=
| 1 |
| 2 |
| d2 |
| 2 |
| d22 |
| 8 |
S3=
| 1 |
| 2 |
| d3 |
| 2 |
| d32 |
| 8 |
由勾股定理可得:
d12+d22=d32,
∴S1+S2=
| π |
| 8 |
| d32 |
| 8 |
所以S1、S2、S3的关系是:S1+S2=S3.
故选A.
点评:本题主要考查运用勾股定理结合图形求面积之间的关系,关键在于根据题意找出直角三角形,运用勾股定理求出三个半圆的直径之间的关系.

练习册系列答案
相关题目
 如图的图案是一次国际数学教育大会(ICME)的会徽,这个会徽图案中蕴藏着许多我们熟悉的数学知识、会徽的主体图案是由一连串如图所示的直角三角形演化而成的,其中OA1=A1A2=A2A3…=A8A9,那么图中第一个小于30°的锐角是( )
如图的图案是一次国际数学教育大会(ICME)的会徽,这个会徽图案中蕴藏着许多我们熟悉的数学知识、会徽的主体图案是由一连串如图所示的直角三角形演化而成的,其中OA1=A1A2=A2A3…=A8A9,那么图中第一个小于30°的锐角是( )| A、∠A2OA3 | B、∠A3OA4 | C、∠A4OA5 | D、∠A5OA6 |
 第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,请你计算OA9的长
第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA1A2是等腰三角形,且OA1=A1A2=A2A3=A3A4=…=A8A9=1,请你计算OA9的长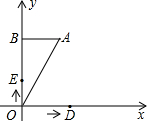 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒. 如图所示,直角三角形ABC中,∠C=90°,AB=5cm,BC=3cm,则以AC为直径的半圆(阴影部分)的面积为( )
如图所示,直角三角形ABC中,∠C=90°,AB=5cm,BC=3cm,则以AC为直径的半圆(阴影部分)的面积为( )