题目内容
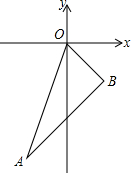 已知如图,在平面直角坐标系中,A(-1,-3),OB=
已知如图,在平面直角坐标系中,A(-1,-3),OB= ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°
(1)求B点坐标;
(2)判断三角形ABO的形状;
(3)求三角形ABO的AO边上的高.
解:(1)设B(x,-x),
则x2+(-x)2=( )2,
)2,
解得x=±1,B在第四象限,
所以B(1,-1);
(2)AO= =
= ,
,
AB= =2
=2 ;
;
而OB2+AB2=AO2,
所以△AOB为直角三角形,且∠ABO=90°;
(3)设三角形ABO的AO边上的高为x,
三角形AOB的面积= AB•OB=
AB•OB= AO•x,
AO•x,
即 ×
× ×
× =
= ×
× x
x
x= .
.
分析:(1)因为OB与x轴所夹锐角是45°,设B(x,-x),利用勾股定理求得即可;
(2)用勾股定理求得AO,AB,用勾股定理逆定理证得直角即可;
(3)利用三角形AOB的面积的计算方法求高.
点评:此题考查勾股定理、勾股定理逆定理的运用,结合面积法求有关直角三角形边的问题.
则x2+(-x)2=(
 )2,
)2,解得x=±1,B在第四象限,
所以B(1,-1);
(2)AO=
 =
= ,
,AB=
 =2
=2 ;
;而OB2+AB2=AO2,
所以△AOB为直角三角形,且∠ABO=90°;
(3)设三角形ABO的AO边上的高为x,
三角形AOB的面积=
 AB•OB=
AB•OB= AO•x,
AO•x,即
 ×
× ×
× =
= ×
× x
xx=
 .
.分析:(1)因为OB与x轴所夹锐角是45°,设B(x,-x),利用勾股定理求得即可;
(2)用勾股定理求得AO,AB,用勾股定理逆定理证得直角即可;
(3)利用三角形AOB的面积的计算方法求高.
点评:此题考查勾股定理、勾股定理逆定理的运用,结合面积法求有关直角三角形边的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
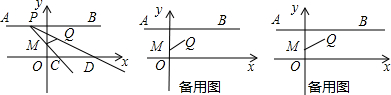
 已知如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8),求P点坐标.
已知如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8),求P点坐标. 已知如图,在平面直角坐标系中,A(-4,0),B(8,0),C(0,8),E为△ABC中AC边上一动点(不和A、C重合),以E为一顶点作矩形EFGH,使G、H点在x轴上,F点在BC上,EF交y轴于D点.并设EH长为x.
已知如图,在平面直角坐标系中,A(-4,0),B(8,0),C(0,8),E为△ABC中AC边上一动点(不和A、C重合),以E为一顶点作矩形EFGH,使G、H点在x轴上,F点在BC上,EF交y轴于D点.并设EH长为x.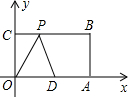 已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为
已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为