题目内容
 已知如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8),求P点坐标.
已知如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8),求P点坐标.
分析:过P作MN的垂线,设垂足为A,根据M、N的坐标和垂径定理,易求得AN、OA的长;若连接PQ,则PQ=OA,由此可求出P点的纵坐标及⊙P的半径;连接PN,在Rt△PAN中,根据勾股定理,即可求出PA的值,即P点的横坐标,由此可求出P点的坐标.
解答: 解:过点P作PA⊥y轴,连接PN,PQ;
解:过点P作PA⊥y轴,连接PN,PQ;
∵⊙P与x轴相切于点Q
∴PQ⊥x轴(1分)
∵M(0,2),N(0,8)
∴OM=2,ON=8,MN=6(2分)
∵PA⊥y轴
∴AN=AM=
MN=3
∴PQ=5(3分)
在Rt△PAN中,∠PAN=90°,
由勾股定理得:PA=
=
=4(4分)
∴P点坐标为(4,5).(5分)
 解:过点P作PA⊥y轴,连接PN,PQ;
解:过点P作PA⊥y轴,连接PN,PQ;∵⊙P与x轴相切于点Q
∴PQ⊥x轴(1分)
∵M(0,2),N(0,8)
∴OM=2,ON=8,MN=6(2分)
∵PA⊥y轴
∴AN=AM=
| 1 |
| 2 |
∴PQ=5(3分)
在Rt△PAN中,∠PAN=90°,
由勾股定理得:PA=
| PN2-AN2 |
| 52-32 |
∴P点坐标为(4,5).(5分)
点评:此题主要考查了切线的性质、勾股定理、垂径定理等知识的综合应用.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
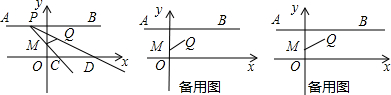
 已知如图,在平面直角坐标系中,A(-4,0),B(8,0),C(0,8),E为△ABC中AC边上一动点(不和A、C重合),以E为一顶点作矩形EFGH,使G、H点在x轴上,F点在BC上,EF交y轴于D点.并设EH长为x.
已知如图,在平面直角坐标系中,A(-4,0),B(8,0),C(0,8),E为△ABC中AC边上一动点(不和A、C重合),以E为一顶点作矩形EFGH,使G、H点在x轴上,F点在BC上,EF交y轴于D点.并设EH长为x.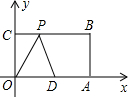 已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为
已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为