Question

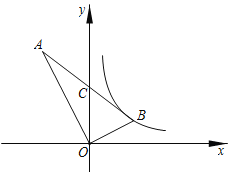
【题目】如图，在平面直角坐标系中，直角△AOB的直角顶点O在坐标原点，OB＝5，OA＝10，斜边AB的中点C恰在y轴上，反比例函数（k＞0）的图象经过点B，则k的值为（　　）

A.10B.C.D.40

Answer 1

【答案】A

【解析】

先利用勾股定理计算出AB＝5，再利用直角三角形斜边上的中线性质得OC＝，则C点坐标为（0，），设B（m，n），利用两点间的距离公式得到m2+n2＝52，m2+（n﹣）2＝（）2，利用加减消元法解得n＝，m＝2，从而得到B点坐标为（2，），然后把B点坐标代入中可求出k的值．

在Rt△AOB中，AB=，

∵点C为斜边AB的中点，

∴OC＝AB＝，

∴C点坐标为（0，），

设B（m，n），

∴m2+n2＝52，m2+（n﹣）2＝（）2，

∴n＝，m＝2，

∴B点坐标为（2，），

把B（2，）代入得k＝2×＝10．

故选：A．