题目内容
给出下列命题:命题1:直线y=x与双曲线y=
| 1 |
| x |
命题2:直线y=8x与双曲线y=
| 2 |
| x |
| 1 |
| 2 |
命题3:直线y=27x与双曲线y=
| 3 |
| x |
| 1 |
| 3 |
命题4:直线y=64x与双曲线y=
| 4 |
| x |
| 1 |
| 4 |
…
(1)请你阅读、观察上面命题,猜想出命题n(n为正整数);
(2)请验证你猜想的命题n是真命题.
分析:(1)根据题意给的数据可得到命题n:直线y=n3x与双曲线y=
有一个交点是(
,n2);
(2)把(
,n2)分别代入直线y=n3x和双曲线y=
中,即可判断命题n是真命题.
| n |
| x |
| 1 |
| n |
(2)把(
| 1 |
| n |
| n |
| x |
解答:解:(1)命题n:直线y=n3x与双曲线y=
有一个交点是(
,n2);
(2)验证如下:
将(
,n2)代入直线y=n3x得:右边=n3×
=n2,左边=n2,
∴左边=右边,
∴点(
,n2)在直线y=n3x上,
同理可证:点(
,n2)在双曲线y=
上,
∴直线y=n3x与双曲线y=
有一个交点是(
,n2).
| n |
| x |
| 1 |
| n |
(2)验证如下:
将(
| 1 |
| n |
| 1 |
| n |
∴左边=右边,
∴点(
| 1 |
| n |
同理可证:点(
| 1 |
| n |
| n |
| x |
∴直线y=n3x与双曲线y=
| n |
| x |
| 1 |
| n |
点评:本题考查了点在图象上,点的横纵坐标满足图象的解析式;也考查了探究规律的方法:从特殊到一般.

练习册系列答案
相关题目
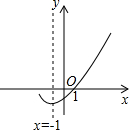 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③a-2b+c>0;④4a-2b+c<0其中正确的命题是
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③a-2b+c>0;④4a-2b+c<0其中正确的命题是