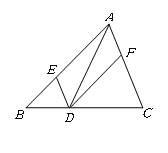Question

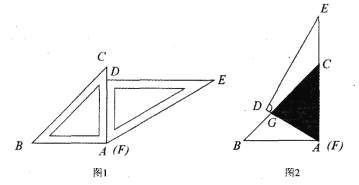
【题目】一副三角板按图 1 所示的位置摆放，将△DEF 绕点 A(F)逆时针旋转 60°后（图 2）， 测得 CG＝8cm，则两个三角形重叠（阴影）部分的面积为（）

A. 16＋16 cm2

B. 16＋ cm2

C. 16＋ cm2

D. 48cm2

Answer 1

【答案】B

【解析】

过G点作GH⊥AC于H，则∠GAC=60°，∠GCA=45°，GC=8cm，先在Rt△GCH中根据等腰直角三角形三边的关系得到GH与CH的值，然后在Rt△AGH中根据含30°的直角三角形三边的关系求得AH，最后利用三角形的面积公式进行计算即可．

解：过G点作GH⊥AC于H，如图，

∠GAC=60°，∠GCA=45°，GC=8cm，
在Rt△GCH中，GH=CH=GC=4cm，
在Rt△AGH中，AH=GH=cm，
∴AC=AH+CH=+4（cm）．
∴两个三角形重叠（阴影）部分的面积=ACGH=×（+4）×4=16+cm2
故选：B．