题目内容
两个小组同时开始登一座450m高的山,第一组的速度是第二组的1.2倍,他们比第二组早15min到达顶峰.两个小组的速度各是多少?如果山高为h m,第一组的攀登速度是第二组的a倍,并比第二组早t min达到顶峰,则两组的攀登速度各是多少?
考点:分式方程的应用
专题:
分析:设第二组的速度为xm/min,则第一组的速度是1.2xm/min,根据第一组比第二组早15min,列方程求解;
把数字代换为字母进一步列出方程解答即可.
把数字代换为字母进一步列出方程解答即可.
解答:解:设第二组的速度为xm/min,则第一组的速度是1.2xm/min,由题意得
-
=15,
解得:x=5,
经检验:x=5是原分式方程的解,且符合题意,
则1.2x=6.
答:第一组的攀登速度6m/min,第二组的攀登速度5m/min.
设第二组的速度为ym/min,则第一组的速度是aym/min,由题意得
-
=t,
解得:y=
,
经检验:y=
是原分式方程的解,且符合题意,
则ay=
.
答:第一组的攀登速度是
m/min,第二组的攀登速度
m/min.
| 450 |
| x |
| 450 |
| 1.2x |
解得:x=5,
经检验:x=5是原分式方程的解,且符合题意,
则1.2x=6.
答:第一组的攀登速度6m/min,第二组的攀登速度5m/min.
设第二组的速度为ym/min,则第一组的速度是aym/min,由题意得
| h |
| y |
| h |
| ay |
解得:y=
| ah-h |
| at |
经检验:y=
| ah-h |
| at |
则ay=
| ah-h |
| t |
答:第一组的攀登速度是
| ah-h |
| t |
| ah-h |
| at |
点评:本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列分式方程求解,注意检验.

练习册系列答案
相关题目
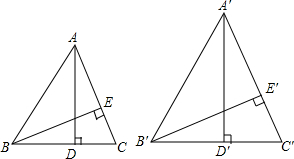 如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证:
如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证: 如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是
如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是 如图,在数轴上表示1,
如图,在数轴上表示1,