��Ŀ����
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() ����
����![]() ��
��![]() ���ϣ���
���ϣ���![]() Ϊֱ����
Ϊֱ����![]() ����
����![]() ��
��![]() ���ϣ����ڵ�
���ϣ����ڵ�![]() �Ϸ�������
�Ϸ�������![]() ��
��![]() ������
������![]() ��
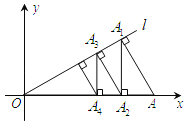
��![]() Ϊ�е㣬�����
Ϊ�е㣬�����![]() �ڵ�һ���ޣ����
�ڵ�һ���ޣ����![]() Ϊ��
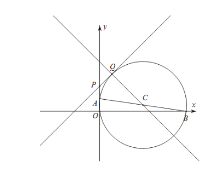
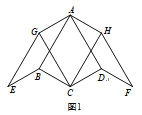
Ϊ��![]() ����㣮���磬ͼ1�е�
����㣮���磬ͼ1�е�![]() Ϊ��
Ϊ��![]() ��һ����㣮
��һ����㣮
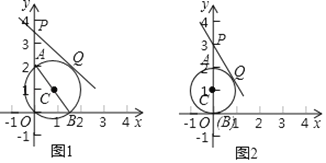
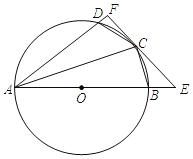
��1����֪��![]() ��
��![]() Ϊ
Ϊ![]() ����㣮
����㣮
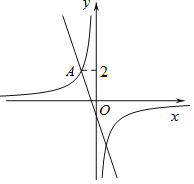
����ͼ2����![]() ����Բ��
����Բ��![]() ������Ϊ__________���߶�
������Ϊ__________���߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
����![]() �����߶�
�����߶�![]() �ij���
�ij���
��2����֪![]() ��ֱ��
��ֱ��![]() ��
��
����![]() ʱ����ֱ��
ʱ����ֱ��![]() �ϴ���
�ϴ���![]() �����
�����![]() �����
�����![]() ������
������![]() �����ֵΪ__________��
�����ֵΪ__________��
����ֱ��![]() ��
��![]() �IJ���Ϊͼ��
�IJ���Ϊͼ��![]() �����ͼ��
�����ͼ��![]() �ϴ���
�ϴ���![]() ����㣬ֱ��д��
����㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�(1)�٣�0��1����![]() ���������������
���������������![]() ���������������2����6��������������ڵ�k��0ʱ��1-2
���������������2����6��������������ڵ�k��0ʱ��1-2![]() <k��
<k��![]() ��k��0ʱ��
��k��0ʱ��![]() ��k<1+2
��k<1+2![]() �������������
�������������
��������
��1������ͼ��֪��C(0��1)����Rt![]() PQC�У�CQ=1��PC=2���ɵ��߶�
PQC�У�CQ=1��PC=2���ɵ��߶�![]() �ij���
�ij���
����ͼ����C��CM��y���ڵ�M������CP��CQ��M(0��1)����Rt![]() ACM�У��ɹ��ɶ����ɵ�CA=
ACM�У��ɹ��ɶ����ɵ�CA=![]() ��CQ=
��CQ=![]() ����Rt
����Rt![]() PCM�У��ɹ��ɶ����ɵ�PC=
PCM�У��ɹ��ɶ����ɵ�PC=![]() ����Rt
����Rt![]() PCQ�У��ɹ��ɶ����ɵ�PQ=
PCQ�У��ɹ��ɶ����ɵ�PQ=![]() ��
��
��2���ٵ�k=1ʱ��y=x+4��Q��t-4��t����P��������Ϊ4ʱ��PQ��ԲC���У���B��m��0������Բ��Ϊ![]() ����CQ��PQ������CQ�Ľ���ʽΪ
����CQ��PQ������CQ�Ľ���ʽΪ![]() ��Q�������Ϊ
��Q�������Ϊ![]() ����C��2t-5��1��������CQ=AC���õ�t=6��t=2��
����C��2t-5��1��������CQ=AC���õ�t=6��t=2��
��y=kx+k+3�������㣨-1��3)��PQ��Բ�����ߣ�AO��Բ���ң�����![]() ����k<0ʱ��Q����ڶ˵㣨-1��3���ͣ�1��2k+3��֮���˶�����P��0��4��ʱ��PQ=2
����k<0ʱ��Q����ڶ˵㣨-1��3���ͣ�1��2k+3��֮���˶�����P��0��4��ʱ��PQ=2![]() ��.��PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4-2
��.��PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4-2![]() ������ʱk=1-2
������ʱk=1-2![]() ����P��0��3��ʱ��PQ=
����P��0��3��ʱ��PQ=![]() ��Q��1��2k+3����
��Q��1��2k+3����![]() ������1-2
������1-2![]() <k��
<k��![]() ����k>0ʱ����P��0��4)ʱ��PQ=2
����k>0ʱ����P��0��4)ʱ��PQ=2![]() ����PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4+2
����PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4+2![]() ������ʱk=1+2
������ʱk=1+2![]() ����P(0��3)ʱ��PQ=
����P(0��3)ʱ��PQ=![]() ��Q��1��2k+3����
��Q��1��2k+3����![]() ��
��![]() ��k<1+2
��k<1+2![]() ��
��
�⣺
��1������ͼ��֪��C��0��1����
��Rt![]() PQC��CQ=1��PC=2��
PQC��CQ=1��PC=2��
��![]() ��
��
�ʴ�Ϊ����0��1����![]() ��
��
����ͼ����C��CM��y���ڵ�M������CP��CQ��
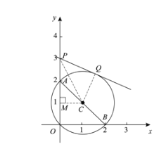
��A��0��2����B��2��0����
��C��1��1����
��M��0��1����
��Rt![]() ACM�У��ɹ��ɶ����ɵ�CA=
ACM�У��ɹ��ɶ����ɵ�CA=![]() ��
��
��CQ=![]() ��
��
��P��0��3����M��0��1����
��PM=2��
��Rt![]() PCM�У��ɹ��ɶ����ɵ�PC=
PCM�У��ɹ��ɶ����ɵ�PC=![]() ��
��
��Rt![]() PCQ�У��ɹ��ɶ����ɵ�PQ=
PCQ�У��ɹ��ɶ����ɵ�PQ=![]() ��
��
��2���ٵ�k=1ʱ��y=x+4��
��Q��t-4��t����
��![]() ��
��
��P��������Ϊ4ʱ��PQ��ԲC���У�
��B��m��0����
��C![]() ��
��
��CQ��PQ��
��CQ�Ľ���ʽΪ![]() ��
��
��Q�������Ϊ![]() ��
��
��![]() ��
��
��m=4t-10��
��C��2t-5��1����
��CQ=AC��
��![]() ��
��
��t=6��t=2��
��t�����ֵΪ6��
�ʴ�Ϊ��6.
�ڡ�-1��x��1��
��y=kx+k+3�������㣨-1��3)��
��PQ��Բ�����ߣ�AO��Բ���ң�
��![]() ��
��
��k<0ʱ��Q����ڶ˵㣨-1��3���ͣ�1��2k+3��֮���˶���
��P��0��4��ʱ��PQ=2![]() ��
��
.��PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4-2![]() ����
����
��ʱk=1-2![]() ��
��
��P��0��3��ʱ��PQ=![]() ��Q��1��2k+3����
��Q��1��2k+3����
��![]() ��
��
��![]() ��
��
��![]() ��
��
��1-2![]() <k��
<k��![]() ��
��
��k>0ʱ����P��0��4)ʱ��PQ=2![]() ��
��
��PΪԲ�ģ�PQ��Ϊ�뾶��Բ��y�ύ�ڵ㣨0��4+2![]() ����
����
��ʱk=1+2![]() ��
��
��P(0��3)ʱ��PQ=![]() ��
��
Q��1��2k+3����
![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��k<1+2
��k<1+2![]() ��
��