题目内容
13. 如图,在正△ABC中,D,E分别是BC,AB上的点,且CD=BE,AD与CE相交于点O.
如图,在正△ABC中,D,E分别是BC,AB上的点,且CD=BE,AD与CE相交于点O.(1)求证:AD=CE;
(2)求∠DOC的度数;
(3)证明:△ABD≌△CAE.
分析 (1)只要证明△ABD≌△CAE即可;
(2)由△ABD≌△CAE,推出∠BAD=∠ACE,推出∠DOC=∠OAC+∠ACE=∠OAC+∠BAD=60°;
(3)(1)中已经证明.
解答 (1)证明: ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠CAE=60°,
∵BE=CD,
∴AE=BD,
在△ABD和△CAE中,
$\left\{\begin{array}{l}{AE=BD}\\{∠B=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE,
∴AD=CE.
(2)∵△ABD≌△CAE,
∴∠BAD=∠ACE,
∴∠DOC=∠OAC+∠ACE=∠OAC+∠BAD=60°.
(3)△ABD≌△CAE见(1)已证.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、三角形的外角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
1.我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3,其中数据899 000用科学记数法表示为( )
| A. | 8.99×104 | B. | 0.899×106 | C. | 899×103 | D. | 8.99×105 |
8.$\frac{1}{2}$-$\frac{1}{6}$-$\frac{1}{12}$-$\frac{1}{20}$-$\frac{1}{30}$=( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{6}$ |
18.甲、乙两人从同一地点出发,同向而行.甲骑自行车,乙步行.如果乙先行12千米,甲用1小时就追上乙;如果乙先走1小时,那么甲只用$\frac{1}{2}$小时就追上乙,则甲的速度是( )
| A. | 6千米/小时 | B. | 12千米/小时 | C. | 18千米/小时 | D. | 36千米/小时 |
2.小壮同学的体重为56.4千克,这个数是四舍五入得来的,那么你认为小壮的体重M千克的范围是( )
| A. | 56.35≤M<56.45 | B. | 56.39<M≤56.44 | C. | 56.41<M<56.50 | D. | 56.44<M<56.59 |
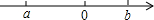 实数a、b在数轴上的位置如图,化简:$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$
实数a、b在数轴上的位置如图,化简:$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{(a-b)^{2}}$