题目内容
 如图,过A、C两点的抛物线y=x2+bx+c上有一点M,已知A(-1,0),C(0,-2),
如图,过A、C两点的抛物线y=x2+bx+c上有一点M,已知A(-1,0),C(0,-2),
(1)这个抛物线的解析式为______;
(2)作⊙M与直线AC相切,切点为C,则M点的坐标为______.
解:(1)将A(-1,0),C(0,-2)的坐标代入y=x2+bx+c得
 ,
,
解得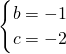 .
.
故此抛物线的解析式为y=x2-x-2;
(2)设直线AC的解析式为y=kx+m,将A(-1,0),C(0,-2)的坐标代入得
 ,
,
解得 .
.
故直线AC的解析式为y=-2x-2,
∵⊙M与直线AC相切,
∴与直线AC垂直的直径所在的直线为y= x+n,
x+n,
∵切点为C,
∴n=-2,
∴与直线AC垂直的直径所在的直线为y= x-2,
x-2,
设M(a,a2-a-2),
则 a-2=a2-a-2,
a-2=a2-a-2,
解得a1=0(舍去),a2=1.5,
∴M(1.5,-1.25).
故答案为:y=x2-x-2,(1.5,-1.25).
分析:(1)由题意根据待定系数法即可求出二次函数的解析式;
(2)由题意根据待定系数法即可求出直线AC的解析式,再根据切线的性质根据待定系数法得到经过M,切点为C的直线解析式,设M(a,a2-a-2),得到关于a的方程,即可求解.
点评:本题考查了抛物线解析式、直线的解析式的求法,切线的性质,互相垂直的两条直线的关系,综合性较强,有一定的难度.
 ,
,解得
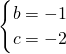 .
.故此抛物线的解析式为y=x2-x-2;
(2)设直线AC的解析式为y=kx+m,将A(-1,0),C(0,-2)的坐标代入得
 ,
,解得
 .
.故直线AC的解析式为y=-2x-2,
∵⊙M与直线AC相切,
∴与直线AC垂直的直径所在的直线为y=
 x+n,
x+n,∵切点为C,
∴n=-2,
∴与直线AC垂直的直径所在的直线为y=
 x-2,
x-2,设M(a,a2-a-2),
则
 a-2=a2-a-2,
a-2=a2-a-2,解得a1=0(舍去),a2=1.5,
∴M(1.5,-1.25).
故答案为:y=x2-x-2,(1.5,-1.25).
分析:(1)由题意根据待定系数法即可求出二次函数的解析式;
(2)由题意根据待定系数法即可求出直线AC的解析式,再根据切线的性质根据待定系数法得到经过M,切点为C的直线解析式,设M(a,a2-a-2),得到关于a的方程,即可求解.
点评:本题考查了抛物线解析式、直线的解析式的求法,切线的性质,互相垂直的两条直线的关系,综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
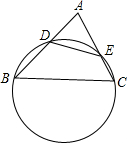 (1)已知:如图,过B、C两点的圆与△ABC的边AB、AC分别相交于点D和点F,且
(1)已知:如图,过B、C两点的圆与△ABC的边AB、AC分别相交于点D和点F,且 如图,过A、C两点的抛物线y=x2+bx+c上有一点M,已知A(-1,0),C(0,-2),
如图,过A、C两点的抛物线y=x2+bx+c上有一点M,已知A(-1,0),C(0,-2),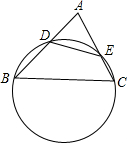 (1)已知:如图,过B、C两点的圆与△ABC的边AB、AC分别相交于点D和点F,且
(1)已知:如图,过B、C两点的圆与△ABC的边AB、AC分别相交于点D和点F,且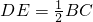 .求证:S△ADE:S四边形DBEC=
.求证:S△ADE:S四边形DBEC= ;
; .求证:S△ADE:S四边形DBEC=
.求证:S△ADE:S四边形DBEC= ;
;