题目内容
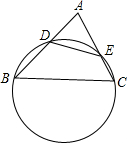（1）已知：如图，过B、C两点的圆与△ABC的边AB、AC分别相交于点D和点F，且DE=| 1 |
| 2 |
| 1 |
| 3 |
（2）在△ABC的外部取一点P（直线BC上的点除外），分别连接PB、PC，∠BPC与∠BAC的大小关系怎样？（不要求证明）
分析：（1）可通过相似三角形根据面积比等于相似比的平方来求解．由于四边形CEDB是圆的内接四边形，可得出三角形ADE和ACB的两组对应角相等，得出这两个三角形相似后，即可得出面积比为1：4，由此可得出本题所求的结论．
（2）如果单纯的比较∠BPC和∠BAC的度数比较困难，如果我们做三角形ABC的外接圆后，可根据点P在三角形外接圆的不同位置来进行比较，就容易多了．
（2）如果单纯的比较∠BPC和∠BAC的度数比较困难，如果我们做三角形ABC的外接圆后，可根据点P在三角形外接圆的不同位置来进行比较，就容易多了．
解答：（1）证明：∵∠ADE、∠AED是圆内接四边形DBCE的外角；
∴∠ADE=∠C，∠AED=∠B．
∴△ADE∽△ACB；
∴S△ADE：S△ACB=DE2：BC2=
；
∴S△ADE：S四边形DBEC=
；
（2）解：作△ABC的外接圆，取点A关于BC的对称点F，作△FBC的外接圆．
①当点P取在弓形BAC内（△ABC外）或弓形BFC内时，∠BPC＞∠BAC；
②当点P取在弧BAC或弧BFC（点A、B、C除外）上时，∠BPC=∠BAC；
③当点P取在弓形BAC与弓形BFC所围成的图形外（除直线BC上的点）时，∠BPC＜∠BAC．
∴∠ADE=∠C，∠AED=∠B．
∴△ADE∽△ACB；
∴S△ADE：S△ACB=DE2：BC2=
| 1 |
| 4 |
∴S△ADE：S四边形DBEC=
| 1 |
| 3 |
（2）解：作△ABC的外接圆，取点A关于BC的对称点F，作△FBC的外接圆．
①当点P取在弓形BAC内（△ABC外）或弓形BFC内时，∠BPC＞∠BAC；
②当点P取在弧BAC或弧BFC（点A、B、C除外）上时，∠BPC=∠BAC；
③当点P取在弓形BAC与弓形BFC所围成的图形外（除直线BC上的点）时，∠BPC＜∠BAC．
点评：本题主要考查了圆周角定理，相似三角形的判定和性质等知识点的应用．
练习册系列答案
相关题目
OAM关于x轴对称，其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点，以点B为顶点且过点D的抛物线l交⊙P与另一点E．
已知：如图，过点C（2，1）分别作x轴、y轴的平行线，交直线y=-x+4于B、A两点，若二次函数y=ax2+bx+c（a≠0）的图象经过坐标原点O，且顶点在矩形ADBC内（包括三边上），则a的取值范围是