题目内容
 如图所示,⊙O是△ABC的外接圆,已知∠ABO=20°,则∠C的度数为
如图所示,⊙O是△ABC的外接圆,已知∠ABO=20°,则∠C的度数为
- A.45°
- B.60°
- C.70°
- D.90°
C
分析:首先连接OA,由OA=OB,根据等边对等角的知识,即可求得∠BAO的度数,然后由三角形内角和定理,可求得∠AOB的度数,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠C的度数.
解答: 解:连接OA,
解:连接OA,
∵OA=OB,
∴∠BAO=∠ABO=20°,
∴∠AOB=180°-∠ABO-∠BAO=140°,
∴∠C= ∠AOB=70°.
∠AOB=70°.
故选C.
点评:此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理.此题难度不大,解题的关键是准确作出辅助线,掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.
分析:首先连接OA,由OA=OB,根据等边对等角的知识,即可求得∠BAO的度数,然后由三角形内角和定理,可求得∠AOB的度数,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠C的度数.
解答:
 解:连接OA,
解:连接OA,∵OA=OB,
∴∠BAO=∠ABO=20°,
∴∠AOB=180°-∠ABO-∠BAO=140°,
∴∠C=
 ∠AOB=70°.
∠AOB=70°.故选C.
点评:此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理.此题难度不大,解题的关键是准确作出辅助线,掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.

练习册系列答案
相关题目
 24、如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
24、如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE. 46、如图所示,AB是直径,D是圆上任意一点,C不与A、B重合,连接BD,并延长得到C,使DC=DB,连接AC,判断△ABC形状.并说明理由.
46、如图所示,AB是直径,D是圆上任意一点,C不与A、B重合,连接BD,并延长得到C,使DC=DB,连接AC,判断△ABC形状.并说明理由.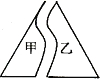 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是 如图所示,AD是△ABC的中线,DF⊥AC,DE⊥AB,垂足分别为F,E,BE=CF.求证:AD平分∠BAC.
如图所示,AD是△ABC的中线,DF⊥AC,DE⊥AB,垂足分别为F,E,BE=CF.求证:AD平分∠BAC.