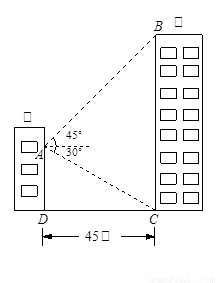题目内容
如图，甲乙两幢楼之间的距离CD等于45米，现在要测乙楼的高BC，（BC⊥CD），所选观察点A在甲楼一窗口处，AD∥BC．从A处测得乙楼顶端B的仰角为45°，底部C的俯角为30°，求乙楼的高度 （取| 3 |
分析：过点A作AE⊥BC于点E，在直角△ACE中利用三角函数求得CE的长，然后在直角△ABE中求得BE的长，即可求解．
解答：
解：过点A作AE⊥BC于点E，在Rt△ACE中
∵∠CAE=30°，AE=DC=45，
∴tan30°=
CE=45×
=15
≈25.5（米）
在Rt△ABE中，∵∠BAE=45°，BE=AE=45，
∴BC=CE+BE=25.5+45=70.5≈71（米）．
解：过点A作AE⊥BC于点E，在Rt△ACE中∵∠CAE=30°，AE=DC=45，
∴tan30°=
| CE |
| 45 |
CE=45×
| ||
| 3 |
| 3 |
在Rt△ABE中，∵∠BAE=45°，BE=AE=45，
∴BC=CE+BE=25.5+45=70.5≈71（米）．
点评：本题考查了仰角与俯角的定义，以及三角函数，正确理解三角函数的定义是关键．
练习册系列答案
相关题目
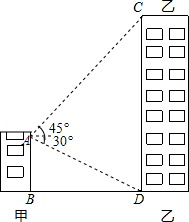（2013•西宁）如图，甲乙两幢楼之间的距离是30米，自甲楼顶A处测得乙楼顶端C处的仰角为45°，测得乙楼底部D处的俯角为30°，则乙楼的高度为
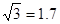，结果精确到1米) .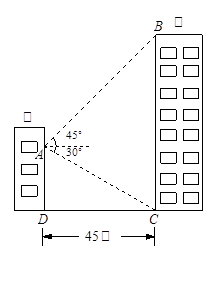
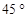，测得乙楼底部D处的俯角为
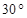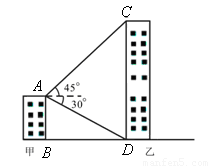
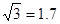，则乙楼的高度为 米.
，结果精确到1米)
.