题目内容
 如图,面积为12cm2的△ABC向x轴正方向平移至△DEF的位置,相应的坐标如图所示(a,b为常数),
如图,面积为12cm2的△ABC向x轴正方向平移至△DEF的位置,相应的坐标如图所示(a,b为常数),(1)求点D、E的坐标;
(2)求四边形ACED的面积.
分析:(1)根据对应点C、F确定出平移距离,再求出CE的长,然后根据平面直角坐标系写出点D、E的坐标即可;
(2)根据梯形的面积公式列式计算即可得解.
(2)根据梯形的面积公式列式计算即可得解.
解答:解:(1)∵△ABC向x轴正方向平移至△DEF的位置,
∴平移距离=CF=-2a,
∴CE=-2a+a=-a,
∴点D(-2a,b),E(-a,0);
(2)由平移性质得,AD∥CE,
所以,四边形ACED的面积=
(-a-2a)b=-
ab.
∴平移距离=CF=-2a,
∴CE=-2a+a=-a,
∴点D(-2a,b),E(-a,0);
(2)由平移性质得,AD∥CE,
所以,四边形ACED的面积=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了坐标与图形变化-平移,熟练掌握平移的性质并求出CE的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
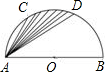 如图,AB为半圆O的直径,点C、D是半圆的三等分点,AB=12cm,则由弦AC、AD和
如图,AB为半圆O的直径,点C、D是半圆的三等分点,AB=12cm,则由弦AC、AD和
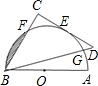 于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处. 所围成的阴影部分的面积为 cm2.
所围成的阴影部分的面积为 cm2.

