Question

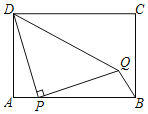
【题目】如图，在矩形中，，，点是边上任意一点（不与点重合），连接，以线段为直角边作等腰直角（点在直线右侧），，连接，则的最小值为_____．

Answer 1

【答案】

【解析】

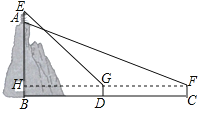
过Q作QE⊥AB于E，在EP上截取EF=EQ，连接QF，根据全等三角形性质得出AF=PE=10，依据△EFQ是等腰直角三角形可得FQ与FB夹角始终为45°，进而得到当BQ⊥FQ时，BQ最小，根据△BQF为等腰直角三角形进一步求解即可得出BQ长度.

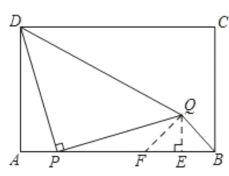
如图所示，过Q作QE⊥AB于E，在EP上截取EF=EQ，连接QF，

∵△DPQ为等腰直角三角形，四边形ABCD为矩形，

∴DP=PQ，∠A=∠PEQ，

易证：∠ADP=∠EPQ，

∴△ADP≌△EPQ(AAS)，

∴AP=QE=EF，AD=PE=10，

∴AF=PE=10，

∵△EFQ为等腰直角三角形，

∴∠QFE=45°，即FQ与FB夹角始终为45°，

∴如图所示，当BQ⊥FQ时，BQ最小，此时△BQF为等腰直角三角形，

又∵QE⊥BF，

∴BE=EF=QE=AP，

∵PE=10，

∴BE=AP=，

∴BF=5，

∴BQ=cos45°BF=

即BQ最小值为

故答案为：