题目内容
如图所示,某旅游景区计划修建一条连接B、C两地的索道.测量人员在山脚A点测得B、C两地的仰角分别为30°和45°,在B地测得C地的仰角为60°,已知C地比A地高1200m,则索道至少需多长?(| 2 |
| 3 |
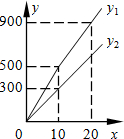
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造方程关系式,进而可解即可求出答案.
解答: 解:如图:∠BAC=∠BCA=45°-30°=15°.
解:如图:∠BAC=∠BCA=45°-30°=15°.
∴BC=AB.
在△BCE与△BAD中,
,
∴△BCE≌△BAD(AAS).
∴BE=BD.
设BC=x,
∵∠CBE=60°,∠BAD=30°.
∴CE=
x,EH=BD=BE=
x.
∵CE+EH=CH=1200,
∴
x+
x=1200.
∴x=1200(
-1)≈879(m).
答:这个景区的索道BC的长至少需约879米.
 解:如图:∠BAC=∠BCA=45°-30°=15°.
解:如图:∠BAC=∠BCA=45°-30°=15°.∴BC=AB.
在△BCE与△BAD中,
|
∴△BCE≌△BAD(AAS).
∴BE=BD.
设BC=x,
∵∠CBE=60°,∠BAD=30°.
∴CE=
| ||
| 2 |
| 1 |
| 2 |
∵CE+EH=CH=1200,
∴
| ||
| 2 |
| 1 |
| 2 |
∴x=1200(
| 3 |
答:这个景区的索道BC的长至少需约879米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.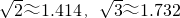 ,结果精确到1m).
,结果精确到1m).
 ,结果精确到1m).
,结果精确到1m).

