题目内容
下列函数解析式中,一定为二次函数的是()
A. y=3x?1 B. y=ax2+bx+c
C. s=2t2+2t+1 D. y=x2+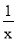
一元二次方程x2﹣2x=0的根是( )
A. x1=0,x2=﹣2 B. x1=1,x2=2 C. x1=1,x2=﹣2 D. x1=0,x2=2
查看答案阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
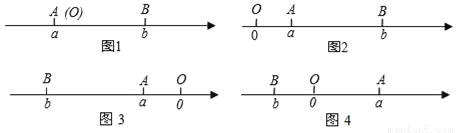
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.
(1)当x=850时,该顾客应选择在 商场购买比较合算;
(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.
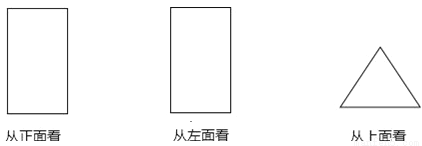
查看答案已知如图为一几何体的三种形状图:
(1)这个几何体的名称为 ;
(2)任意画出它的一种表面展开图;
(3)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自A地出发到收工时,行走记录为(单位:千米):+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3,回答下列问题
(1)收工时小王在A地的哪边?距A地多少千米?
(2)若每千米耗油0.2升,问从A地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离A地多远?
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案小文统计了本班同学一周的体育锻练情况,并绘制了直方图
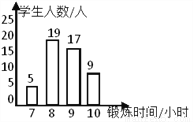
①小文同学一共统计了60人;
②这个班同学一周参加体育锻炼时间的众数是8;
③这个班同学一周参加体育锻炼时间的中位数是9;
④这个班同学一周参加体育锻炼时间的平均值为8.
根据图中信息,上述说法中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
B 【解析】小文同学一共统计了5+19+17+9=50人,故①错; 数据8出现了19次,最多,为众数,故②正确; 在第25位,26位的均是9,所以9为中位数,③正确; 这个班同学一周参加体育锻炼时间的平均值为(5×7+19×8+17×9+9×10)=8.6, ④错; 故选:B.下列因式分解正确的是( )
A. 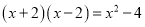 B.
B. 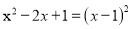
C. 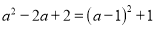 D.
D. 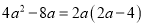
若把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
A.  B.
B. 
C. 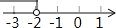 D.
D. 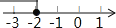
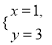 是二元一次方程
是二元一次方程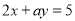 的一个解,则a的值为( )
的一个解,则a的值为( )
A. 1 B. 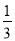 C. 3 D. -1
C. 3 D. -1
下列计算正确的是( )
A. 2a+3a=6a B. a2+a3=a5 C. a8÷a2=a6 D. (a3)4= a7
查看答案已知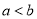 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. 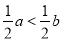 B.
B. 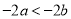 C.
C. 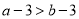 D.
D. 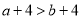
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是_____%.
20 【解析】设该药品平均每次降价的百分率为x,根据降价后的价格=降价前的价格(1-降价的百分率),则第一次降价后的价格是25(1-x),第二次后的价格是25(1-x)2,据此即可列方程求解. 【解析】 设该药品平均每次降价的百分率为x, 由题意可知经过连续两次降价,现在售价每盒16元, 故25(1-x)2=16, 解得x=0.2或1.8(不合题意,舍去), 故该药品平均每次...已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=____.
查看答案若一元二次方程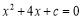 有两个不相等的实数根,则c的值可以是 (写出一个即可).
有两个不相等的实数根,则c的值可以是 (写出一个即可).
抛物线y=2x2﹣3x+4与y轴的交点坐标是______.
查看答案如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )
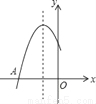
A. ②④ B. ①④ C. ②③ D. ①③
查看答案设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
关于x的一元二次方程x2﹣3x+m=0没有实数根,则实数m的取值范围为( )
A.  B.
B.  C.
C.  D.
D. 
抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为( )
A. y=3x2+2x-5 B. y=3x2+2x-4 C. y=3x2+2x+3 D. y=3x2+2x+4
查看答案要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.  x(x+1)=28 B.
x(x+1)=28 B.  x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
已知x1、x2是一元二次方程x2﹣4x+1=0的两个根,则x1+x2等于( )
A.﹣4 B.﹣1 C.1 D.4
查看答案抛物线y=2x2-3的顶点在( )
A. 第一象限 B. 第二象限 C. x轴上 D. y轴
查看答案下列函数解析式中,一定为二次函数的是()
A. y=3x?1 B. y=ax2+bx+c
C. s=2t2+2t+1 D. y=x2+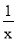
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自A地出发到收工时,行走记录为(单位:千米):+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3,回答下列问题
(1)收工时小王在A地的哪边?距A地多少千米?
(2)若每千米耗油0.2升,问从A地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离A地多远?
(1)收工时小王在A地的东边,距A地3千米;(2)从A地出发到收工时,共耗油10.2升;(3)小王最远离A地9千米. 【解析】试题分析:将各数进行相加求和,正数就是在A地东边,负数就是在A地西边;将各数的绝对值进行求和,然后乘以0.2得出答案;分别求出每次离A地的距离,然后进行比较大小. 试题解析:(1)、8+(-9)+7+(-2)+5+(-10)+7+(-3)=3 即收工时小王...化简与求值:
(1)化简: 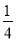 (﹣4x2+2x﹣8)﹣(
(﹣4x2+2x﹣8)﹣(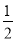 x﹣1)
x﹣1)
(2)先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣2ab2﹣2,其中a=﹣2,b=2.
查看答案计算:
(1)16÷(﹣23)﹣(﹣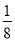 )×(﹣4)
)×(﹣4)
(2)﹣4﹣(﹣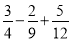 )÷
)÷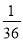
(3)﹣14﹣[2﹣(﹣3)2]÷(﹣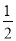 )3.
)3.
《庄子.天下篇》中写道:“一尺之棰,日取其半,万世不竭”意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图.

由图易得: 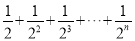 =_____.
=_____.
小明与小刚规定了一种新运算*:若a、b是有理数,则a*b=3a﹣2b.小明计算出2*5=﹣4,请你帮小刚计算2*(﹣5)=_____.
查看答案若x2+x=2,则(x2+2x)﹣(x+1)值是_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
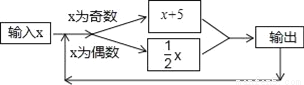
A. 3 B. 6 C. 4 D. 2
D 【解析】根据运算程序得到:除去前两个结果24,12,剩下的以6,3,8,4,2,1循环, ∵(2017-2)÷6=335…5, 则第2017次输出的结果为2, 故选D.下列是由一些火柴搭成的图案:图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第5个图案用多少根火柴棒( )
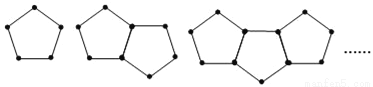
A. 20 B. 21 C. 22 D. 23
查看答案多项式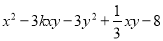 合并同类项后不含xy项,则k的值是( )
合并同类项后不含xy项,则k的值是( )
A. 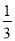 B.
B. 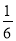 C.
C. 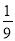 D. 0
D. 0
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
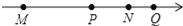
A. 点M B. 点N C. 点P D. 点Q
查看答案下列说法,其中正确的个数为( )
①正数和负数统称为有理数;
②一个有理数不是整数就是分数;
③有最小的负数,没有最大的正数;
④符号相反的两个数互为相反数;
⑤﹣a一定在原点的左边.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案下列各题去括号所得结果正确的是( )
A. x2﹣(x﹣y+2z)=x2﹣x+y+2z B. x﹣(﹣2x+3y﹣1)=x+2x﹣3y+1
C. 3x﹣[5x﹣(x﹣1)]=3x﹣5x﹣x+1 D. (x﹣1)﹣(x2﹣2)=x﹣1﹣x2﹣2
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
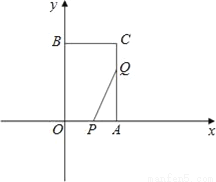
如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm2?
(2)△PAQ的面积能否达到3cm2?
(3)经过多长时间,P、Q两点之间的距离为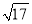 cm?
cm?
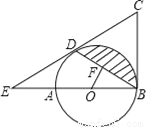
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
查看答案已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
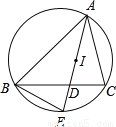
查看答案如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.求证:IE=BE.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列说法正确的是( )
A. 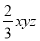 与
与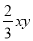 是同类项 B.
是同类项 B. 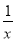 和
和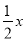 是同类项
是同类项
C. 0.5x3y2与7x2y3是同类项 D. 5m2n与﹣4nm2是同类项
D 【解析】试题分析:如果两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项.A选项中所含的字母不相同;B选项中第一个不是单项式,而是分式;C、相同字母的指数不相同;D是同类项,故选D.下列各式中,等号不成立的是( )
A. |﹣4|=4 B. ﹣|4|=|﹣4| C. |﹣4|=|4| D. ﹣|﹣4|=﹣4
查看答案下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣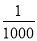 >0 C. ﹣
>0 C. ﹣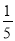 <﹣
<﹣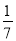 D.
D. 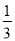 <0.3
<0.3
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣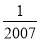 C.
C. 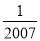 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案(1)阅读理【解析】
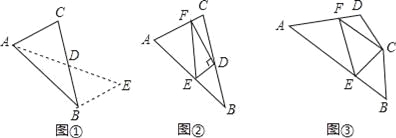
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


 x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )