题目内容
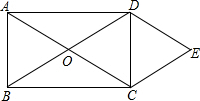 如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.(1)请你判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
分析:(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,
(2)由矩形的性质可知四边形OCED的面积为矩形ABCD面积的一半,问题得解.
(2)由矩形的性质可知四边形OCED的面积为矩形ABCD面积的一半,问题得解.
解答:解:(1)四边形OCED的形状是菱形,
理由如下:
∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OD=OC,
∴四边形CODE是菱形;
(2)∵AB=6,BC=8,
∴矩形ABCD的面积=6×8=48,
∵S△ODC=
S矩形ABCD=12,
∴四边形OCED的面积=2S△ODC=24.
理由如下:
∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OD=OC,
∴四边形CODE是菱形;
(2)∵AB=6,BC=8,
∴矩形ABCD的面积=6×8=48,
∵S△ODC=
| 1 |
| 4 |
∴四边形OCED的面积=2S△ODC=24.
点评:此题考查了菱形的判定与性质以及矩形的性质.此题难度不大,注意证得四边形CODE是菱形是解此题的关键.

练习册系列答案
相关题目
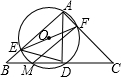 如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③
如图,已知△ABC为等腰直角三角形,D为斜边BC的中点,经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M.对于如下五个结论:①∠FMC=45°;②AE+AF=AB;③| ED |
| EF |
| BA |
| BC |
| A、2个 | B、3个 | C、4个 | D、5个 |
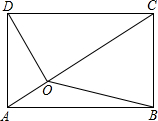 如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为( )
如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为( )| A、2 | ||
B、2
| ||
C、2
| ||
| D、3 |
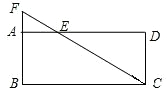 如图,已知E是矩形ABCD的边AD上的点,AE:ED=1:3,CE与BA的延长线交于点F.如果三角形AEF的面积为1,那么四边形ABCD的面积为
如图,已知E是矩形ABCD的边AD上的点,AE:ED=1:3,CE与BA的延长线交于点F.如果三角形AEF的面积为1,那么四边形ABCD的面积为