题目内容
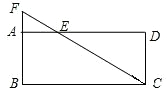如图，已知E是矩形ABCD的边AD上的点，AE：ED=1：3，CE与BA的延长线交于点F．如果三角形AEF的面积为1，那么四边形ABCD的面积为分析：根据相似三角形的性质，可求CD、AD，即可求四边形ABCD的面积．
解答：解：设AE=a，则ED=3a，
设AF=b，三角形AEF的面积为1，即
ab=1，则ab=2，
根据AB∥CD，得到△AEF∽△DEC，
∴
=
=
，
∴CD=3b，AD=4a，
四边形ABCD的面积为4a•3b=12ab=24．
设AF=b，三角形AEF的面积为1，即
| 1 |
| 2 |
根据AB∥CD，得到△AEF∽△DEC，
∴
| AF |
| CD |
| AE |
| DE |
| 1 |
| 3 |
∴CD=3b，AD=4a，
四边形ABCD的面积为4a•3b=12ab=24．
点评：本题主要运用了相似三角形的性质，相似三角形的对应边的比相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
24、如图，已知P是矩形ABCD的内的一点．求证：PA2+PC2=PB2+PD2．
22、如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．
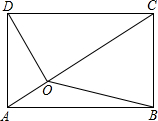如图，已知O是矩形ABCD内一点，且OA=1，OB=3，OC=4，那么OD的长为（ ）| A、2 | ||
B、2
| ||
C、2
| ||
| D、3 |
