题目内容
如图,正方形OA1B1C1的边长为1,以O为圆心、OA1为半径作扇形OA1C1,弧A1C1与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,弧A2C2与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;…按此规律继续作下去,则阴影部分面积S10为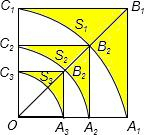
分析:正方形OA1B1C1的边长为1,则S正方形OA1B1C1=1,OB1=
,以O为圆心,OA为半径作扇形OA1C1,得到S1=1-S扇形OA1C1=1-
;以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,得到S2=
-S扇形OA2C2=
-
;依此类推得到Sn=
-
.进而可将n=10代入求解.
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 8 |
| 1 |
| 2n-1 |
| π |
| 2n+1 |
解答:解:S10=
-
=
-
.
故答案为
-
.
| 1 |
| 210-1 |
| π |
| 210+1 |
=
| 1 |
| 29 |
| π |
| 211 |
故答案为
| 1 |
| 29 |
| π |
| 211 |
点评:本题考查了扇形面积的计算以及正方形的性质,要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为5,P为DC上一点,设DP=x,△APD的面积为y,关于y与x的函数关系式为:y=
如图,正方形ABCD的边长为5,P为DC上一点,设DP=x,△APD的面积为y,关于y与x的函数关系式为:y= 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边为a1=1,按上述方法所作的正方形的边长依次为a2、a3、a4、…an,根据以上规律写出
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边为a1=1,按上述方法所作的正方形的边长依次为a2、a3、a4、…an,根据以上规律写出 如图,正方形的周长为8cm,则矩形EFBG的周长为
如图,正方形的周长为8cm,则矩形EFBG的周长为 如图,正方形ABCD,BE⊥ED,连接BD,CE.
如图,正方形ABCD,BE⊥ED,连接BD,CE. 如图,正方形网格中的每个小正方形的边长都是1,△ABC的顶点都在格点上,请在给定的网格中按画图:
如图,正方形网格中的每个小正方形的边长都是1,△ABC的顶点都在格点上,请在给定的网格中按画图: