Question

【题目】在平面直角坐标系中，直线交轴于点，交轴于点，抛物线经过点，与直线交于点．

（1）求抛物线的解析式；

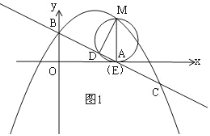
（2）如图，横坐标为的点在直线上方的抛物线上，过点作轴交直线于点，以为直径的圆交直线于另一点．当点在轴上时，求的周长；

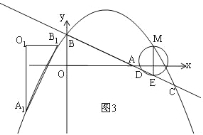
（3）将绕坐标平面内的某一点按顺时针方向旋转，得到，点的对应点分别是．若的两个顶点恰好落在抛物线上，请直接写出点的坐标．

Answer 1

【答案】（1）抛物线的解析式为：y=﹣x2+x+1；

（2）△DEM的周长= ；

（3）点A1（ ， ）或（﹣， ）．

【解析】

试题分析：（1）利用待定系数法求抛物线的解析式；

（2）如图1，A与E重合，根据直线y=﹣x+1求得与x轴交点坐标可得OA的长，由勾股定理得AB的长，利用等角的三角函数得：sin∠ABO= ，cos∠ABO= ，则可得DE和DM的长，根据M的横坐标代入抛物线的解析式可得纵坐标，即ME的长，相加得△DEM的周长；

（3）由旋转可知：O1A1⊥x轴，O1B1⊥y轴，设点A1的横坐标为x，则点B1的横坐标为x+1，所以点O1，A1不可能同时落在抛物线上，分以下两种情况：

①如图2，当点O1，B1同时落在抛物线上时，根据点O1，B1的纵坐标相等列方程可得结论；

②如图3，当点A1，B1同时落在抛物线上时，根据点B1的纵坐标比点A1的纵坐标大 ，列方程可得结论．

试题解析：（1）∵直线y=﹣x+1交y轴于点B，∴B（0，1），

∵抛物线y=﹣x2+bx+c经过点B和点C（4，﹣2）．∴ ，解得： ，

∴抛物线的解析式为：y=﹣x2+x+1；

（2）如图1，∵直线y=﹣x+1交x轴于点A，

当y=0时，﹣ x+1=0，x=，∴A（，0），∴OA=，

在Rt△AOB中，∵OB=1，∴AB= ，∴sin∠ABO=，cos∠ABO=，

∵ME∥x轴，

∴∠DEM=∠ABO，

∵以ME为直径的圆交直线BC于另一点D，

∴∠EDM=90°，

∴DE=MEcos∠DEM=ME，DM=MEsin∠DEM=ME，

当点E在x轴上时，E和A重合，则m=OA=，

当x=时，y=﹣ ×（）2+×+1= ；∴ME=，

∴DE= = ，DM= =，

∴△DEM的周长=DE+DM+ME= = ；

（3）由旋转可知：O1A1⊥x轴，O1B1⊥y轴，设点A1的横坐标为x，则点B1的横坐标为x+1，

∵O1A1⊥x轴，

∴点O1，A1不可能同时落在抛物线上，分以下两种情况：

①如图2，当点O1，B1同时落在抛物线上时，

点O1，B1的纵坐标相等，

∴﹣x2+x+1=﹣（x+1）2+（x+1）+1，

解得：x= ，

此时点A1的坐标为（ ， ），

②如图3，当点A1，B1同时落在抛物线上时，

点B1的纵坐标比点A1的纵坐标大，

﹣x2+x+1+ =﹣（x+1）2+（x+1）+1，

解得：x=﹣，

此时A1（﹣， ），

综上所述，点A1（ ， ）或（﹣， ）．