题目内容
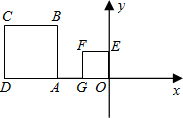 如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是
如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是分析:两个位似图形的主要特征是:每对位似对应点与位似中心共线;不经过位似中心的对应线段平行.则位似中心就是两对对应点的延长线的交点,本题分两种情况讨论即可.
解答:解:①当两个位似图形在位似中心同旁时,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,将C(-4,2),F(-1,1)代入,得
,
解得
即y=-
x+
,
令y=0得x=2,
∴O′坐标是(2,0);
②当位似中心O′在两个正方形之间时,
可求直线OC解析式为y=-
x,直线DE解析式为y=
x+1,
联立
,解得
,
即O′(-
,
).
故本题答案为:(2,0)或(-
,
).
设直线CF解析式为y=kx+b,将C(-4,2),F(-1,1)代入,得
|
解得
|
| 1 |
| 3 |
| 2 |
| 3 |
令y=0得x=2,
∴O′坐标是(2,0);
②当位似中心O′在两个正方形之间时,
可求直线OC解析式为y=-
| 1 |
| 2 |
| 1 |
| 4 |
联立
|
|
即O′(-
| 4 |
| 3 |
| 2 |
| 3 |
故本题答案为:(2,0)或(-
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查位似图形的性质,难度一般,注意掌握每对位似对应点与位似中心共线,另外解答本题注意分情况讨论,避免漏解.

练习册系列答案
相关题目
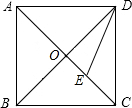 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|


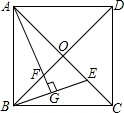
 如图所示,正方形ABCD中,O为对角线的交点,CF平分∠ACD,延长CD至G,使DG=DF,连接AG,交CF延长线于E,连OE、OD,交CF于H,有以下结论:①△ADG≌△CDF;②OE∥CG;③CH=EH;④CE⊥AG,其中正确的有
如图所示,正方形ABCD中,O为对角线的交点,CF平分∠ACD,延长CD至G,使DG=DF,连接AG,交CF延长线于E,连OE、OD,交CF于H,有以下结论:①△ADG≌△CDF;②OE∥CG;③CH=EH;④CE⊥AG,其中正确的有