题目内容
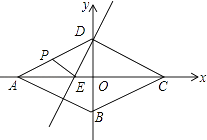
【题目】如图,点O是边长为4 ![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= .
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= . 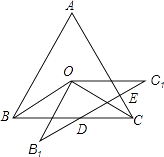
【答案】6﹣2 ![]()
【解析】解:令OB1与BC的交点为F,B1C1与AC的交点为M,过点F作FN⊥OB于点N,如图所示. 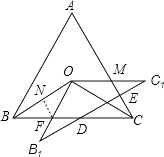
∵将△OBC绕点O逆时针旋转30°得到△OB1C1 ,
∴∠BOF=30°,
∵点O是边长为4 ![]() 的等边△ABC的内心,
的等边△ABC的内心,
∴∠OBF=30°,OB= ![]() AB=4,
AB=4,
∴△FOB为等腰三角形,BN= ![]() OB=2,
OB=2,
∴BF= ![]() =
= ![]() =OF.
=OF.
∵∠OBF=∠OB1D,∠BFO=∠B1FD,
∴△BFO∽△B1FD,
∴ ![]() .
.
∵B1F=OB1﹣OF=4﹣ ![]() ,
,
∴B1D=4 ![]() ﹣4.
﹣4.
在△BFO和△CMO中,有 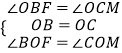 ,
,
∴△BFO≌△CMO(ASA),
∴OM=BF= ![]() ,C1M=4﹣
,C1M=4﹣ ![]() ,
,
在△C1ME中,∠C1ME=∠MOC+∠MCO=60°,∠C1=30°,
∴∠C1EM=90°,
∴C1E=C1Msin∠C1ME=(4﹣ ![]() )×
)× ![]() =2
=2 ![]() ﹣2.
﹣2.
∴DE=B1C1﹣B1D﹣C1E=4 ![]() ﹣(4
﹣(4 ![]() ﹣4)﹣(2
﹣4)﹣(2 ![]() ﹣2)=6﹣2
﹣2)=6﹣2 ![]() .
.
所以答案是:6﹣2 ![]() .
.
【考点精析】通过灵活运用等边三角形的性质和三角形的内切圆与内心,掌握等边三角形的三个角都相等并且每个角都是60°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心即可以解答此题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目